“Prof. Julio Stern sobre o Prof. Carlos Alberto de Bragança Pereira - FBST Full Bayesian Significance Test. Me ensinou quase toda a estatística que eu sei (isso foi fácil) depois de des-ensinar quase toda a estatística que eu pensava que sabia (bem mais difícil)!”

  • Pesquisa dos professores Carlos A. de B. Perreira e Julio M. Stern, com principais desenvolvimentos no período de 1999 e 2009
  • Proposta inicialmente publicada na revista Entropy em 1999 1
  • Proposta “consolidada” com a publicação na revista Bayesian Analysis em 20082

A ideia

“Fornecer uma teoria intuitiva, coerente e conveniente para acessar a significância estatística de hipóteses precisas.”3

A metodologia FBST baseia-se na avaliação de ev(H|X), ou e-value evidência da hipótese precisa H sob a obtenção da amostra X. Ainda conforme4, esta metodologia com suporte no e-value apresenta propriedades desejáveis como:

  1. Fornecer uma funcão de suporte à (ou medida de significância estatística da) hipótese em teste, idealmente uma medida de probabilidade no espaço paramétrico original ou natural do problema;

  2. Ter uma definicão intrinsecamente geométrica, independente de qualquer aspecto não geométrico, como a particular parametrizaçao da hipótese sendo testada, ou o particular sistema de coordenadas escolhido para o espaço paramétrico, i.e., ser um procedimento invariante;

  3. Fornecer uma função de suporte que seja suave, i.e. contínua e diferenciável, nos parâmetros da hipótese e nas estatísticas da amostra, dentro de condições apropriadas de regularidade do modelo;

  4. Obedecer ao princípio da verossimilhança, i.e. a informação obtida das observações deve ser representada pela, e apenas pela, função de verossimilhança;

  5. Não requerer qualquer artifício ad hoc, como dar probabilidades positivas a conjuntos de medida nula, ou estabelecer razões de crença iniciais arbitrárias entre hipóteses;

  6. Ser uma função de suporte possibilística, onde o suporte a uma disjunção lógica é o máximo entre o suporte dos disjuntos;

  7. Ser um procedimento exato, i.e., não utilizar na definição do e-valor qualquer aproximação assintótica;

  8. Fornecer um teste consistente para uma dada hipótese precisa;

  9. Fornecer operações de composicionalidade para modelos complexos;

  10. Permitir a incorporação de experiência prévia ou opiniões de especialistas via distribuições a priori.

Veja o material original de Julio Stern 5, onde para cada propriedade listada, uma publicação que a embasa é apresentada.

O método

Definições

\(\Xi\): Espaço amostral; \(\Delta\): Espaço observável; \(\Theta\): Espaço paramétrico.

Hipótese precisa H, (\(\,g(\theta) \leq c \wedge h(\theta) = c\, , \textrm{sendo } c \textrm{ uma constante})\), tal que, \(\Theta_0 = \{\theta \in \Theta: H\}\).

\(f(\theta | d)\) é a densidade posteriori obtida.

\(T_\varphi = \{ \theta \in \Theta \mid f(\theta | d) > \varphi \}\), subespaço paramétrico onde a densidade posteriori é superior a \(\varphi\)

\(\mathbf{k}(T_\varphi) = \int_{T_\varphi} f(\theta | d)d\theta\) é a credibilidade de \(T_\varphi\) na posteriori.

Algoritmo

  1. Encontre \(\theta^* = \arg \underset{\theta \in \Theta_0}{\max}f(\theta | d)\)

  2. Obtenha a densidade posteriori no ponto \(\theta^*\), \(f^* = f(\theta^* | d )\)

  3. Obtenha o subespaço \(T* = T_{f^*}\)

  4. Calcule a credibilidade de \(\mathbf{k}^* = \mathbf{k}(T_{f^*})\)

  5. Calcule o e-value sobre H dado X, \(ev(H | X) = 1 - \mathbf{k}^*\)

Ilustração

Exemplo 6.3 apresentado no artigo publicado na Bayesian Analysis6

No gif abaixo têm-se a ilustração da metodologia FBST aplicada a um conjunto de dados distribuídos normalmente com \(\mu\) e \(\tau\) desconhecidos. Atribuindo uma priori extremamente vaga ao vetor de parâmetros, i.e \((\mu, \tau) \in \Re \times \Re\), obtemos a densidade posteriori:

\[ f(\mu, \tau) = \tau^{6.5} \exp \left \{ -\frac{15\tau(\mu - 0.9)^2}{2} \right \} \]

As hipóteses precisas a serem testadas são:

  • \(H_0: \quad \mu = 1.1\) ( Conjunto \(\Theta_0\))
  • \(H_1: \quad \tau = 2.5\) ( Conjunto \(\Theta_1\))
  • \(H_2: \quad cv = \mu\sqrt{\tau} = 0.5\) ( Conjunto \(\Theta_2\))

Exemplos

Intenção de voto

##======================================================================
## Obtendo a priori

betaPrior <- function(P, LI, LS, CONF = 0.80) {
    ## P = proporção ("estimativa" pontual)
    ## LI, LS = limite inferior e superior para proporção
    ## CONF = confiança do intervalo descritvo
    fobj <- function(alpha) {
        beta <- (alpha * (1 - P) - 1 + 2 * P)/P
        prob <- diff(pbeta(q = c(LI, LS), alpha, beta))
        (prob - CONF)^2
    }
    alpha <- optimize(fobj, c(1, 100))$minimum
    beta <- (alpha * (1 - P) - 1 + 2 * P)/P
    return(list(alpha = alpha, beta = beta))
}

(prior <- betaPrior(0.525, 0.4, 0.65, 0.95))
## $alpha
## [1] 31.38933
## 
## $beta
## [1] 28.4951
##======================================================================
## Obtendo a verossimilhanca

y <- 24  ## Numero de eleitores com intenção de votar no atual prefeito
n <- 80  ## Numero de eleitores consultados
(veros <- list(alpha = y + 1, beta = n - y + 1))
## $alpha
## [1] 25
## 
## $beta
## [1] 57
##======================================================================
## Obtendo a posteriori (analiticamente)
(poste <- list(alpha = y + prior$alpha, beta = n - y + prior$beta))
## $alpha
## [1] 55.38933
## 
## $beta
## [1] 84.4951
(mode <- with(poste, (alpha - 1)/(alpha + beta - 2)))
## [1] 0.3944559
##======================================================================
## Resultado da análise
par(lwd = 2, bty = "n")
with(poste,   curve(dbeta(x, alpha, beta), from = 0, to = 1))
with(prior, curve(dbeta(x, alpha, beta), add = TRUE, lty = 3, col = 4))
with(veros, curve(dbeta(x, alpha, beta), add = TRUE, lty = 3, col = 2))
legend("topright", col = c(1, 2, 4), lty = 1:3, bty = "n",
       legend = c("Posteriori", "Verossimilhança", "Priori"))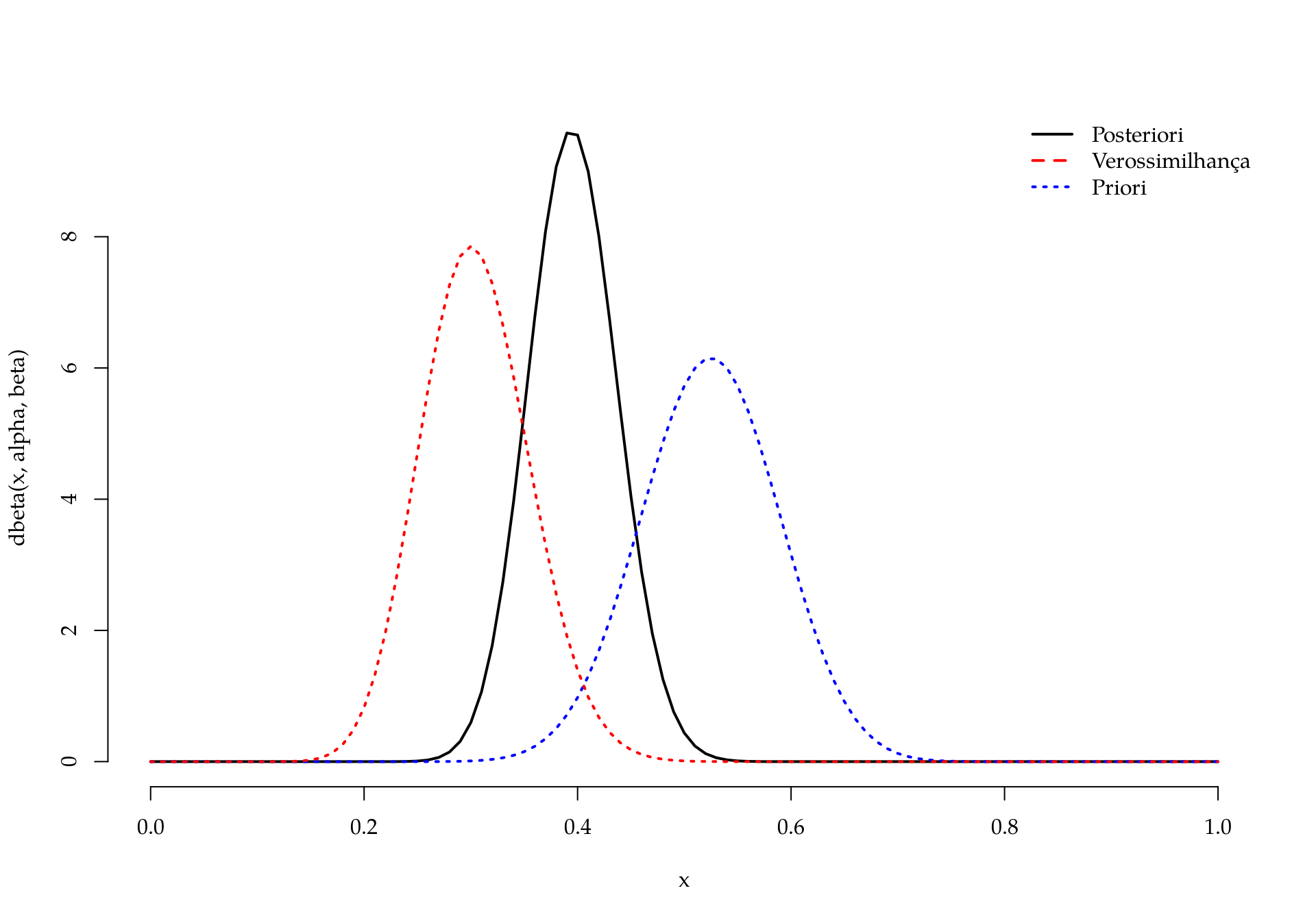

Testando as hipóteses \(H_0: \theta = 3\) contra \(H_1: \theta \neq 3\)

attach(poste)

## FBST para exemplo simples (muito simples)

theta0 <- 0.3
f0 <- dbeta(theta0, alpha, beta)
t02 <- uniroot(function(x) dbeta(x, alpha, beta) - f0,
               interval = c(0.4, 1))
(T0 <- c(0.3, t02$root))
## [1] 0.3000000 0.4945294
(k0 <- diff(pbeta(T0, alpha, beta)))
## [1] 0.9823365
(ev <- 1 - k0)
## [1] 0.01766348
## Graficamente
curve(dbeta(x, alpha, beta), xlab = expression(theta), lwd = 2)
abline(v = theta0, col = 4, lty = 2, lwd = 2)
##
abline(h = f0, col = 5)
##
abline(v = T0, col = 4, lty = 2, lwd = 2)
##
x <- seq(T0[1], T0[2], length.out = 100)
fx <- dbeta(x, alpha, beta)
polygon(c(x, rev(x)),
        c(fx, rep(0, length(fx))),
        col="gray70")
abline(v = mode, col = 2, lty = 2)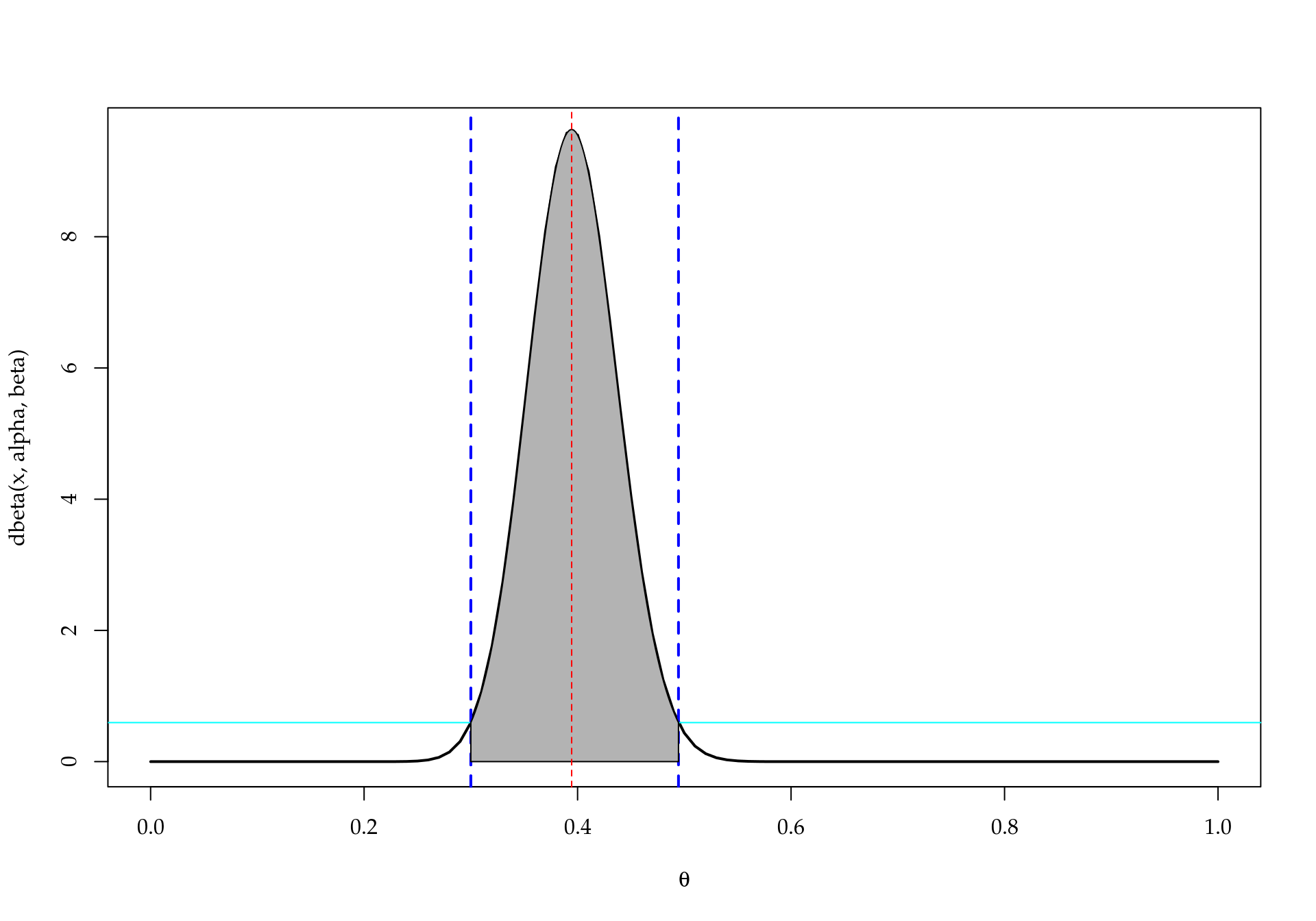

detach(poste)

Avaliando o “poder do teste” com os dados do exemplo, supondo que o \(\theta\) “”verdadeiro“” seja o valor modal da posteriori.

## Função para calcular o valor de evidência FBST, especifico ao
## problema verossimilhança Binomial, priori Beta

f.ev <- function(theta, posterior) {
    with(posterior, {
        f0 <- dbeta(theta, alpha, beta)
        T0 <- rootSolve::uniroot.all(
            function(x) dbeta(x, alpha, beta) - f0,
            interval = c(0, 1))
        if (length(T0) == 0) {
            return(evalor = 1)
        } else {
            k0 <- diff(pbeta(T0, alpha, beta))
            ev <- 1 - abs(k0)
            return(evalor = ev)
        }
    })
}

thetas <- seq(0, 1, length.out = 100)
evalues <- unlist(sapply(thetas, f.ev, posterior = poste))

plot(y = 1 - evalues, x = thetas, type = "l",
     xlab = expression(Theta[0]),
     ylab = "k* = 1 - e-values")
abline(v = mode, col = 4, lty = 2)
rug(thetas)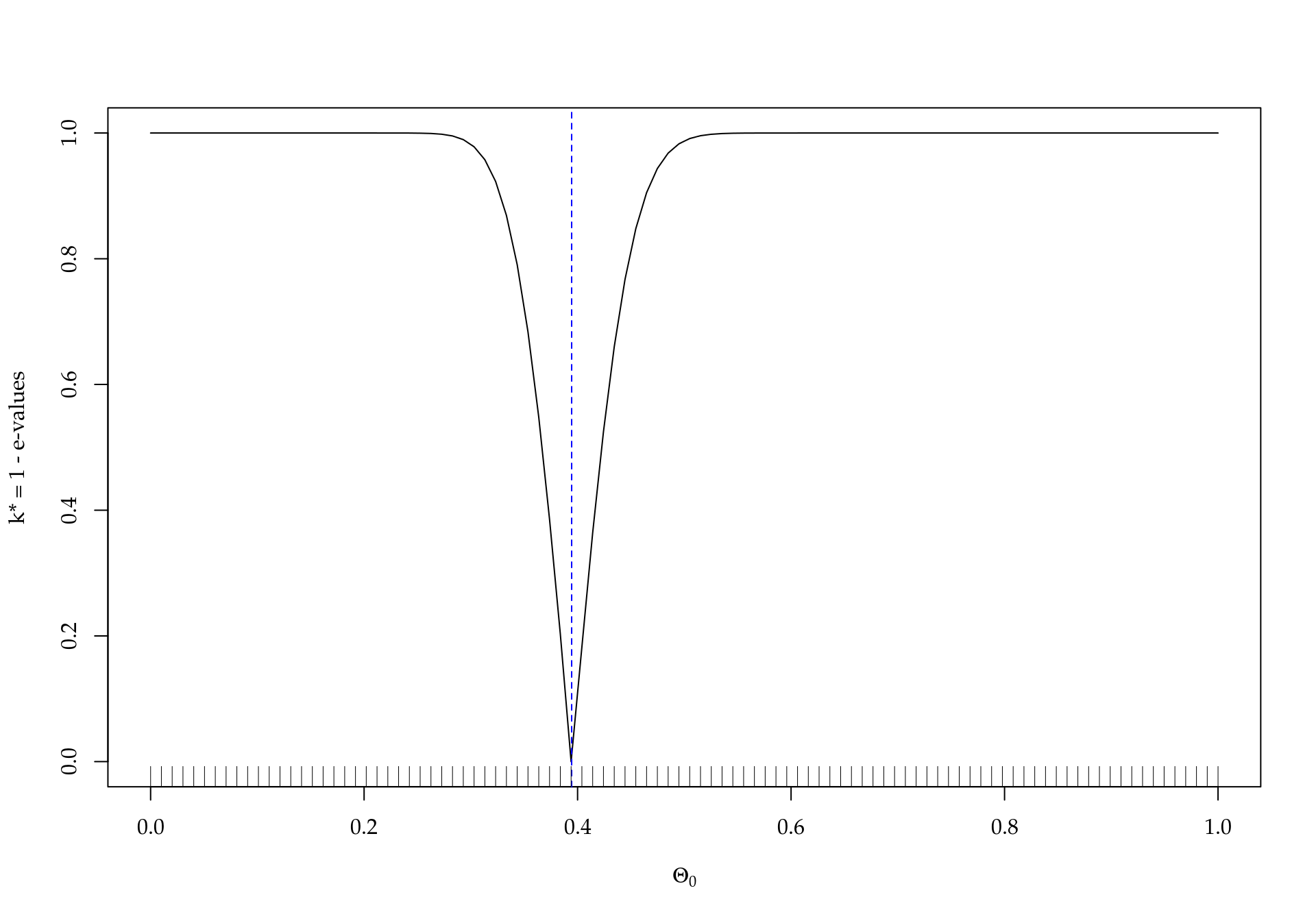

Materiais consultados

  1. Artigo que propõe o FBST http://www.mdpi.org/entropy/papers/e1040099.pdf↩

  2. Artigo que consolida a metodologia FBST http://computacao.br/~jstern/papers/papersJS/jsbayan1.pdf↩

  3. Aula de Erudição (Textos de memorial por Julio Stern) https://www.ime.usp.br/~jstern/vitae/jmst2.pdf (texto pleno)↩

  4. Aula de Erudição (Textos de memorial por Julio Stern) https://www.ime.usp.br/~jstern/vitae/jmst2.pdf (texto pleno)↩

  5. Aula de Erudição (Textos de memorial por Julio Stern) https://www.ime.usp.br/~jstern/vitae/jmst2.pdf (texto pleno)↩

  6. Artigo que consolida a metodologia FBST http://computacao.br/~jstern/papers/papersJS/jsbayan1.pdf↩


© Copyright 2016 Ribeiro Jr., E. E.