O problema

(P-valor subjetivo) Para uma moeda honesta têm-se probabilidade 1/2 de obtenção de “cara” ou “coroa”. Um grupo de alunos encontrou uma moeda com um pequena deformação e decidiram avaliar estatisticamente a hipótese de que a moeda permanece honesta. Primeiramente João levou a moeda para casa e decidiu jogá-la 20 vezes obtendo 6 caras. Maria, no outro dia, ficou com a moeda para avaliar a hipótese, ela realizou lançamentos até observar 6 caras, necessitou-se de 20. No terceiro dia José foi realizar o experimento para testar a hipótese, ele decidiu realizar os lançamentos durante a noite, foram 20 lançamentos feitos até que sua mãe o chamou para jantar, ele havia obtido 6 caras. Calcule os p-valores para a hipótese em teste para cada experimento e conclua a respeito da hipótese sob um nível de significância de 0.05.

Análise frequentista

Estudando a parametrização da binomial negativa

##-------------------------------------------
dnegbin <- function(x, k, prob) {
    ## Parametrização onde x = número de tentativas até se obter k
    ## sucessos. th é a probabilidade de sucesso
    (choose(x - 1, k - 1) * prob^k * (1 - prob)^(x - k)) *
        ! x == 0
}

## Estudando a parametrização da função nativa do R
dnegbin(20, 6, 0.5)
## [1] 0.01108932
dnbinom(14, 6, 0.5)
## [1] 0.01108932

Análise dos experimentos via testes de hipóteses

## Informações do experimento
n <- 20
y <- 6
prob <- 0.5

## p-valor para o experimento Binomial
(pv1 <- pbinom(y, size = n, prob = prob))
## [1] 0.05765915
## p-valor para o experimento Binomial-Negativo
(pv2 <- pnbinom(n - y - 1, size = y, prob = prob, lower = FALSE))
## [1] 0.03178406
##-------------------------------------------
## Parametros graficos
x <- 0:n
px1 <- dbinom(x, size = n, prob = prob)
px2 <- dnbinom(x, size = y, prob = prob)
ylim <- c(0, max(px1, px2))

par(mfrow = c(1, 2), mar = c(4, 3, 3, 3))
plot(px1 ~ x, type = "h", ylim = ylim, lwd = 3)
lines(px1[1:(y + 1)] ~ x[1:(y + 1)],
      type = "h", lwd = 4, col = "blue")
legend("topleft", bty = "n", fill = "blue",
       legend = substitute(
           P(X[B]<=~q)==Pr,
           list(q = y, Pr = round(pv1, 3))))
plot(px2 ~ x, type = "h", ylim = ylim, lwd = 3)
lines(px2[(n - y):n] ~ x[(n - y):n],
      type = "h", lwd = 4, col = "blue")
legend("topleft", bty = "n", fill = "blue",
       legend = substitute(
           P(X[BN]>=~q)==Pr,
           list(q = n - y, Pr = round(pv2, 3))))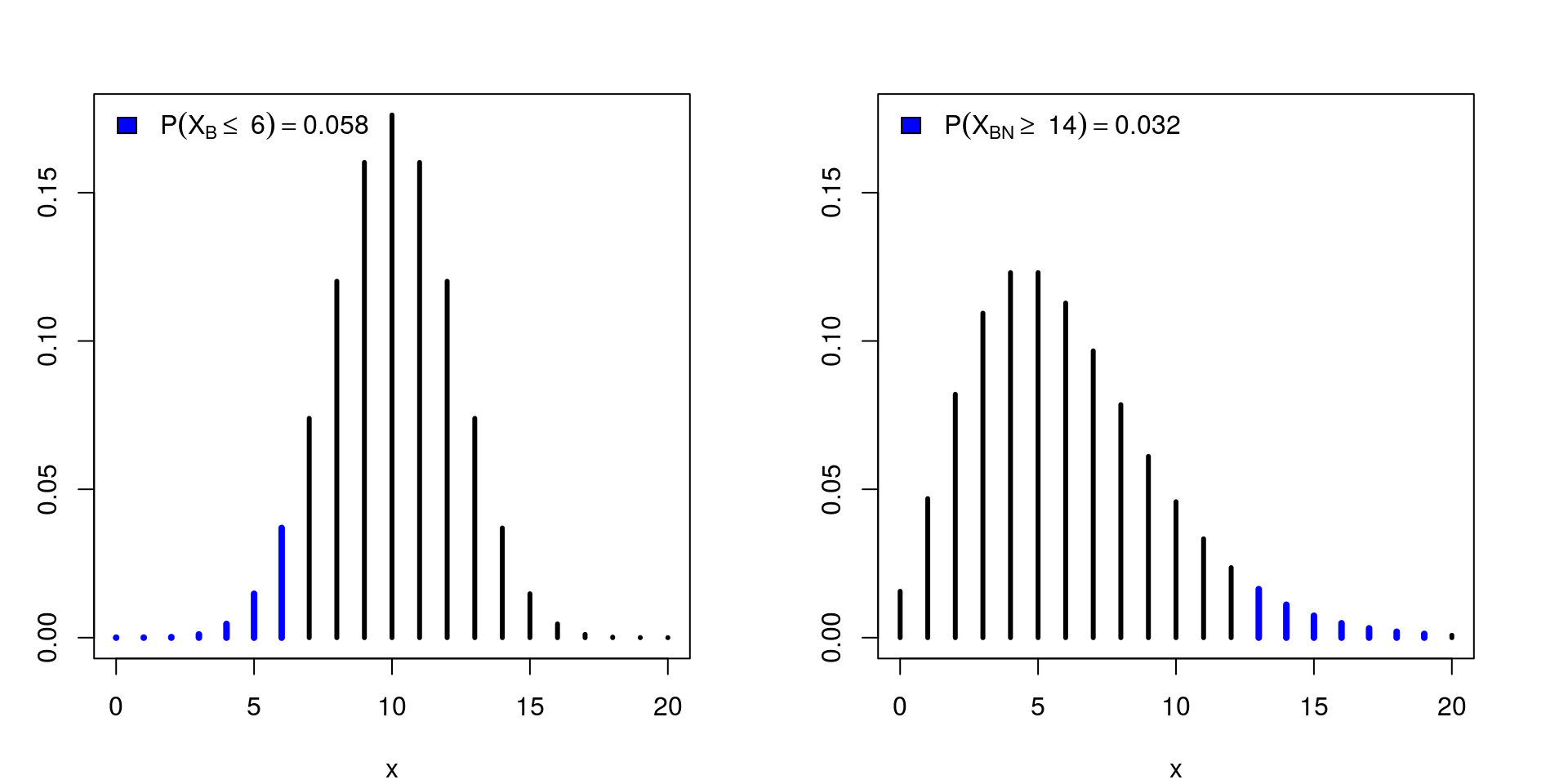

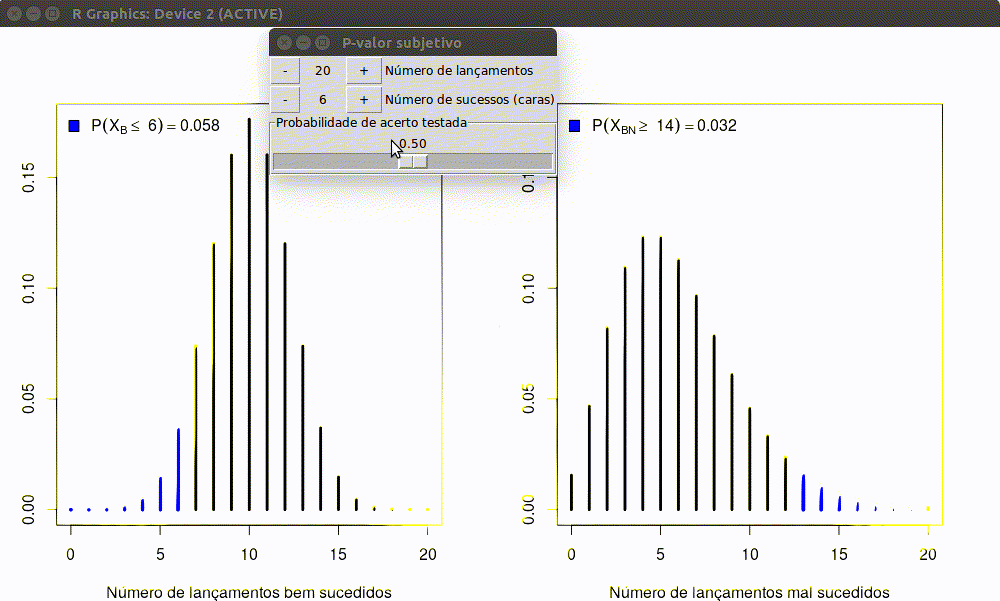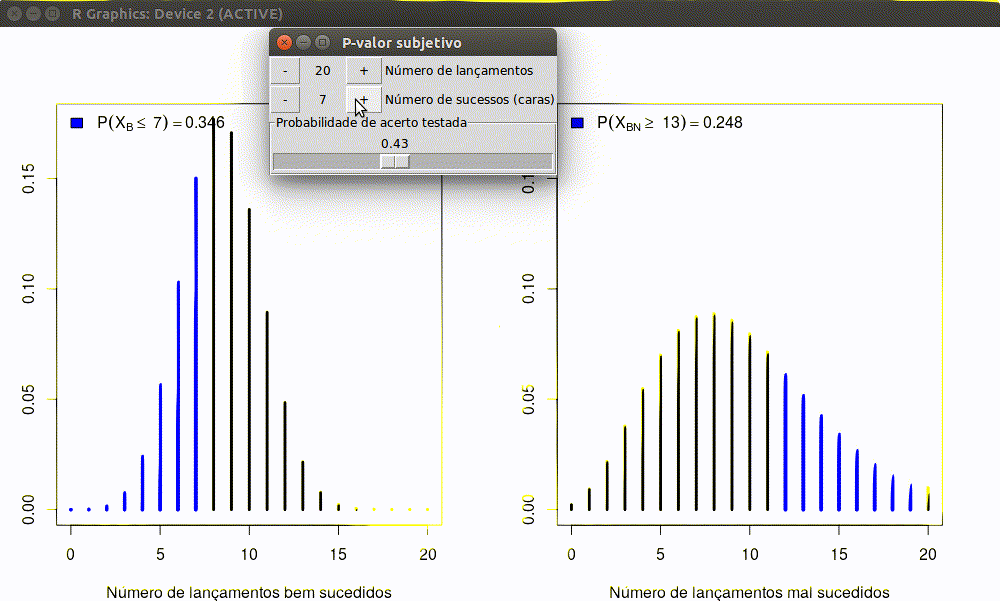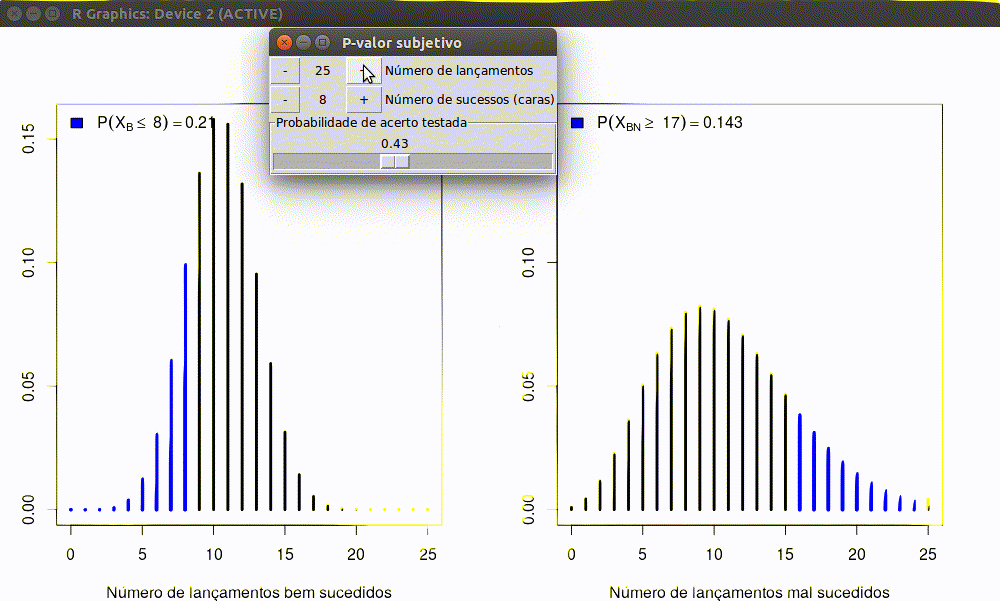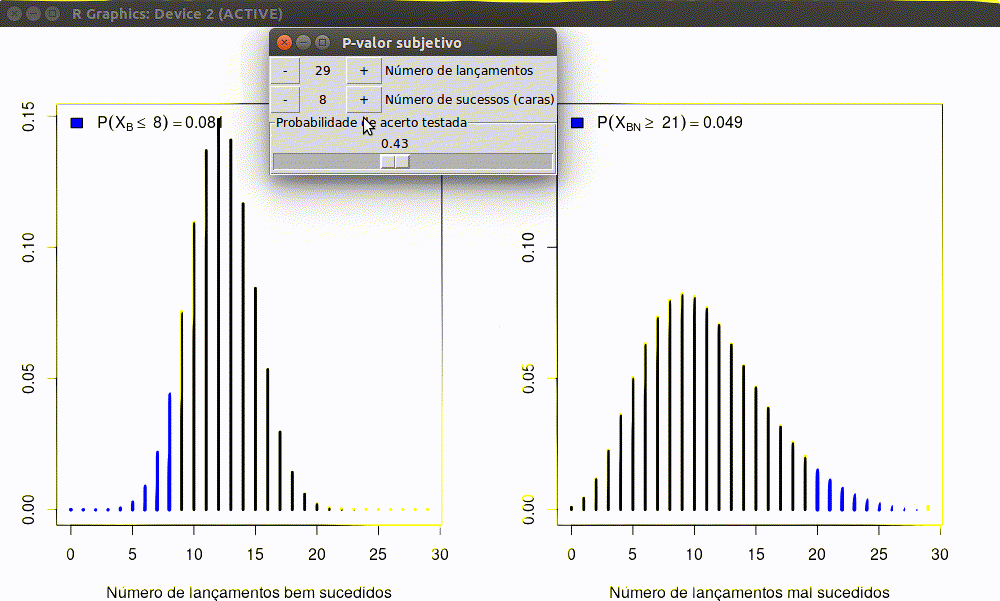
Note que mesmo que Maria e João tenham obtido o mesmo resultado, as conclusões a partir de testes de hipóteses, a um nível de significância de 5%, são distintas. Isso se deve ao fato de que sob o paradigma frequentista leva-se em consideração o processo de amostragem e as demais possíveis amostras. No entanto esse paradigma fere o princípio da verossimilhança uma vez que obtidos os mesmos dados a informação acerca do parâmetro desconhecido (a probabilidade) deve ser a mesma!

Uma ilustração iterativa de como as coisas discordam é exibida abaixo.

##----------------------------------------------------------------------
## Interface interativa

library(rpanel)

rp.pvalor <- function() {
    action <- function(input) {
        with(input, {
            if (n < y) {
                layout(1)
                plot(0, type = "n", axes = FALSE, xlab = "", ylab = "")
                text(0, 0.2, "Informações incorretas\ndo experimento",
                     cex = 2, col = "red")
            } else {
                ## Probabilidades associadas
                x <- 0:n
                px1 <- dbinom(x, size = n, prob = prob)
                px2 <- dnbinom(x, size = y, prob = prob)
                pv1 <- pbinom(y, size = n, prob = prob)
                pv2 <- pnbinom(n - y - 1, size = y, prob = prob,
                               lower = FALSE)
                ylim <- c(0, max(px1, px2))
                ## Gráficos
                par(mfrow = c(1, 2), mar = c(4, 3, 4, 3))
                plot(px1 ~ x, type = "h", ylim = ylim, lwd = 3,
                     xlab = "Número de lançamentos bem sucedidos")
                lines(px1[1:(y + 1)] ~ x[1:(y + 1)],
                      type = "h", lwd = 4, col = "blue")
                legend("topleft", bty = "n", fill = "blue",
                       legend = substitute(
                           P(X[B]<=~q)==Pr,
                           list(q = y, Pr = round(pv1, 3))))
                plot(px2 ~ x, type = "h", ylim = ylim, lwd = 3,
                     xlab = "Número de lançamentos mal sucedidos")
                lines(px2[(n - y):n] ~ x[(n - y):n],
                      type = "h", lwd = 4, col = "blue")
                legend("topleft", bty = "n", fill = "blue",
                       legend = substitute(
                           P(X[BN]>=~q)==Pr,
                           list(q = n - y, Pr = round(pv2, 3))))
            }
        })
        return(input)
    }
    ## Cria a interface
    panel <- rp.control(title = "P-valor subjetivo")
    rp.doublebutton(panel, n, step = 1, showvalue = TRUE,
                    action = action, range = c(0, 80), initval = 20,
                    title = "Número de lançamentos")
    rp.doublebutton(panel, y, step = 1, showvalue = TRUE,
                    action = action, range = c(0, 80), initval = 6,
                    title = "Número de sucessos (caras)")
    rp.slider(panel, prob, from = 0.01, to = 0.99, initval = 0.5,
              resolution = 0.01, action = action, showvalue = TRUE,
              title = "Probabilidade de acerto testada")
    invisible()
}

rp.pvalor()

© Copyright 2016 Ribeiro Jr., E. E.