Implementações em R

Neste trabalho utilizaremos o software R pela praticidade e por ser software estatístico mais utilizado pela comunidade. No R diversos pacotes são destinado a Machine Learning e Statistical Learning, como pode ser visto em Cran Task Views.

Aqui, seguindo as recomendações do texto base da disciplina An Introduction to Statistical Learning, utilizaremos o pacote e1071 que é uma implementação em R baseada na LIBSVM.

## Pacote principal
library(e1071)

##-------------------------------------------
## Outros pacotes
## library(LiblineaR)
## library(klaR)
## library(kernlab)
## library(rdetools)

Conjunto de dados

Para a aplicação dos métodos de classificação via SVM serão utilizados os dados OJ (Oranje Juice) do pacote ISLR (pacote complementar do livro-texto da disciplina). Esses dados reference a 1070 observações sobre compra de sucos de laranja em um mercado. Os registros contemplam a informação de interesse, suco comprado CC para Citrus Hill e MM Minute Maid e demais 17 características sobre o cliente e produto.

##======================================================================
## Os dados
## help(OJ, h = "html")
data(OJ, package = "ISLR")
str(OJ)

## 'data.frame':    1070 obs. of  18 variables:
##  $ Purchase      : Factor w/ 2 levels "CH","MM": 1 1 1 2 1 1 1 1 1 1 ...
##  $ WeekofPurchase: num  237 239 245 227 228 230 232 234 235 238 ...
##  $ StoreID       : num  1 1 1 1 7 7 7 7 7 7 ...
##  $ PriceCH       : num  1.75 1.75 1.86 1.69 1.69 1.69 1.69 1.75 1.75 1.75 ...
##  $ PriceMM       : num  1.99 1.99 2.09 1.69 1.69 1.99 1.99 1.99 1.99 1.99 ...
##  $ DiscCH        : num  0 0 0.17 0 0 0 0 0 0 0 ...
##  $ DiscMM        : num  0 0.3 0 0 0 0 0.4 0.4 0.4 0.4 ...
##  $ SpecialCH     : num  0 0 0 0 0 0 1 1 0 0 ...
##  $ SpecialMM     : num  0 1 0 0 0 1 1 0 0 0 ...
##  $ LoyalCH       : num  0.5 0.6 0.68 0.4 0.957 ...
##  $ SalePriceMM   : num  1.99 1.69 2.09 1.69 1.69 1.99 1.59 1.59 1.59 1.59 ...
##  $ SalePriceCH   : num  1.75 1.75 1.69 1.69 1.69 1.69 1.69 1.75 1.75 1.75 ...
##  $ PriceDiff     : num  0.24 -0.06 0.4 0 0 0.3 -0.1 -0.16 -0.16 -0.16 ...
##  $ Store7        : Factor w/ 2 levels "No","Yes": 1 1 1 1 2 2 2 2 2 2 ...
##  $ PctDiscMM     : num  0 0.151 0 0 0 ...
##  $ PctDiscCH     : num  0 0 0.0914 0 0 ...
##  $ ListPriceDiff : num  0.24 0.24 0.23 0 0 0.3 0.3 0.24 0.24 0.24 ...
##  $ STORE         : num  1 1 1 1 0 0 0 0 0 0 ...

O exercício da obtenção de um classificador para esse conjunto de dados também foi proposto no exercício 8, pág. 371 de An Introduction to Statistical Learning. Seguindo as orientações do exercício particionaremos a base de dados em OJ.te e OJ.tr, as bases de teste e treino respectivamente. 800 observações serão tomadas para treino.

##----------------------------------------------------------------------
## Separando os dados em teste e treino
set.seed(2016)
index <- sample(nrow(OJ), 800)
OJ.tr <- OJ[index, ]
OJ.te <- OJ[-index, ]

A seguir serão propostos classificadores com base em SVM, considerando kernel linear (que adotando um valor de custo para classificações incorretas, tem o nome de Support Vector Classifiers), polynomial, radial e sigmoid.

Métodos de classificação

A função e1071::svm(...) é a função destinada à determinação dos vetores de suporte. O pacote e1071 provém também diversos métodos para obtenção de resultados do classificador definido pela svm.

Nas próximas seções todos os ajustes dos classificadores são realizados via função svm. Abaixo é exibido os argumentos da função.

## Para determinar o classificador
## help(svm, h = "html")
args(e1071:::svm.default)

## function (x, y = NULL, scale = TRUE, type = NULL, kernel = "radial", 
##     degree = 3, gamma = if (is.vector(x)) 1 else 1/ncol(x), coef0 = 0, 
##     cost = 1, nu = 0.5, class.weights = NULL, cachesize = 40, 
##     tolerance = 0.001, epsilon = 0.1, shrinking = TRUE, cross = 0, 
##     probability = FALSE, fitted = TRUE, ..., subset, na.action = na.omit) 
## NULL

Para comparação dos classificadores serão utilizados inspeções visuais da curva ROC, bem como os resultados obtidos pela classificação. Para exibição dos resultados a função compareROC foi implementada.

##======================================================================
## Funções utéis

library(Epi)
compareROC <- function(models) {
    ## Models uma lista nomeada com os resultados da função ROC do
    ## modelos classificadores a serem comparados
    tableC <- sapply(models,
                     FUN = function(roc) {
                         index <- with(roc$res,
                                       which.max(sens + spec))
                         round(cbind(roc$res[index, ],
                                     "AUC" = roc$AUC), 4)
                     })
    rownames(tableC) <- c("sens", "spec", "pvp", "pvn", "prob", "AUC")
    return(tableC)
}

SVM kernel linear

\[ K(x_i, x_k) = \left \langle x_i, \, x_k \right \rangle \]

##-------------------------------------------
## Classificador default
(c0l <- svm(Purchase ~ ., kernel = "linear", data = OJ.tr,
           probability = TRUE))

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "linear", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  linear 
##        cost:  1 
##       gamma:  0.05555556 
## 
## Number of Support Vectors:  331

## Resumo do classificador
summary(c0l)

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "linear", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  linear 
##        cost:  1 
##       gamma:  0.05555556 
## 
## Number of Support Vectors:  331
## 
##  ( 167 164 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  CH MM

## Tabela de classificação no treino
pred.tr0l <- predict(c0l, newdata = OJ.tr, probability = TRUE)
table(pred.tr0l, OJ.tr$Purchase)

##          
## pred.tr0l  CH  MM
##        CH 442  81
##        MM  55 222

## Tabela de classificação no teste
pred.te0l <- predict(c0l, newdata = OJ.te, probability = TRUE)
table(pred.te0l, OJ.te$Purchase)

##          
## pred.te0l  CH  MM
##        CH 137  21
##        MM  19  93

## Probabilidades associadas as decisões
probs.tr0l <- attr(pred.tr0l, "probabilities")[, 2]
probs.te0l <- attr(pred.te0l, "probabilities")[, 2]

## Curvas ROC
par(mfrow = c(1, 2))
roc.te0l <- ROC(test = probs.tr0l, stat = OJ.tr$Purchase, plot = "ROC")
roc.tr0l <- ROC(test = probs.te0l, stat = OJ.te$Purchase, plot = "ROC")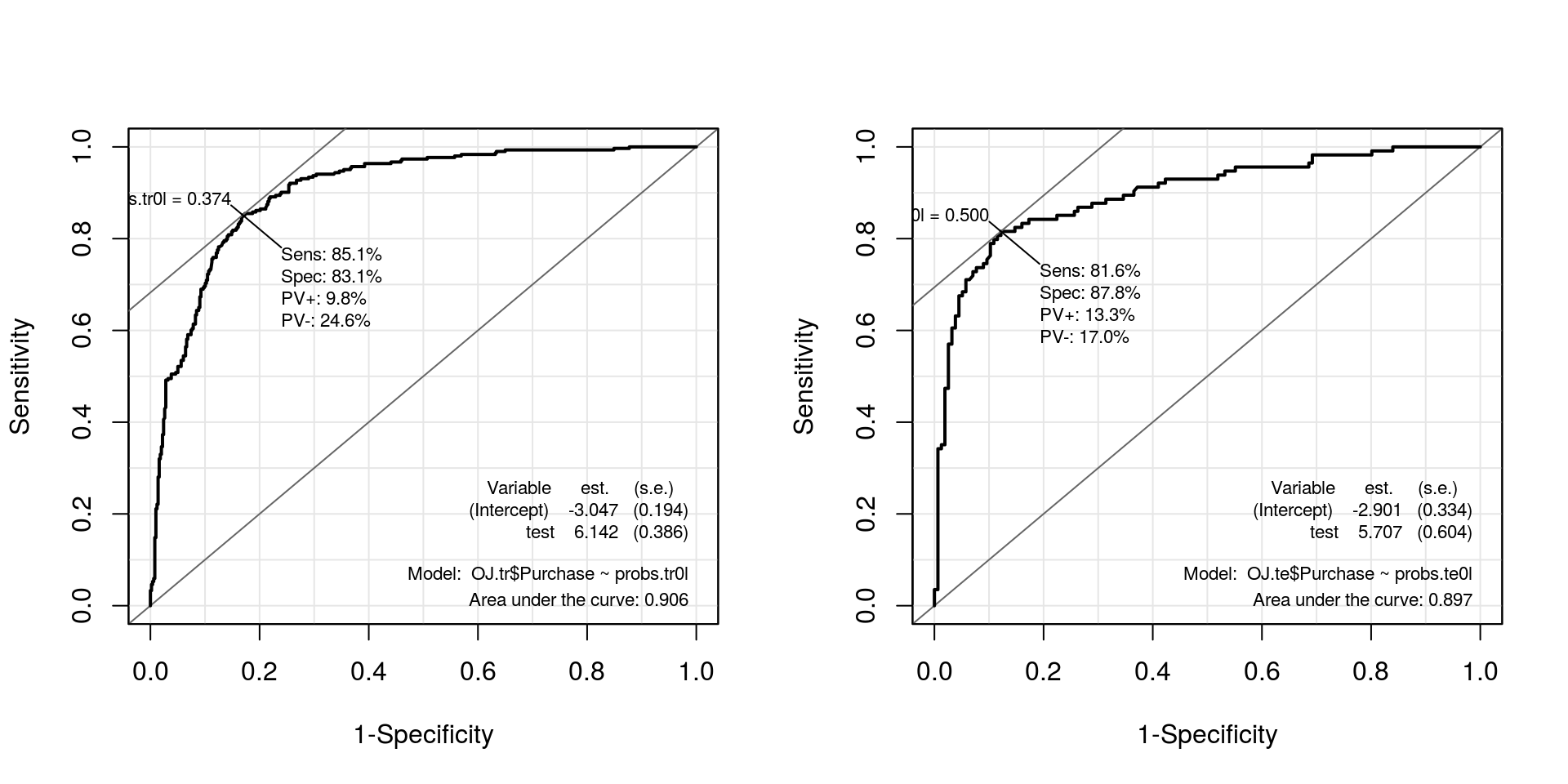

Perceba que a função svm define alguns argumentos sem que o usuário precise especificá-los. Pelo default da função o método, denominado em sala como Maximal Margin Classifier. Abaixo definidos diferentes valores para o “custo” (que define quantos vetores de suportes serão utilizados na definição da fronteira).

Comparação de classificadores via validação cruzada Cuidado o tuning é realizado via validação cruzada sob simulação assim diferentes realizações da função geram diferentes resultados. O refinamento dos parâmetros considerados para validação cruzada pode ser feito em tune.control().

## Cuidado !
set.seed(2016)
(svm.tune <- tune(svm, Purchase ~ ., data = OJ.tr, kernel = "linear",
                  ranges = list(cost = c(0.001, 0.5, 1, 10))))

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost
##   0.5
## 
## - best performance: 0.17375

summary(svm.tune)

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost
##   0.5
## 
## - best performance: 0.17375 
## 
## - Detailed performance results:
##    cost   error dispersion
## 1 1e-03 0.34625 0.05104804
## 2 5e-01 0.17375 0.03458584
## 3 1e+00 0.17375 0.03458584
## 4 1e+01 0.18000 0.04005205

plot(svm.tune)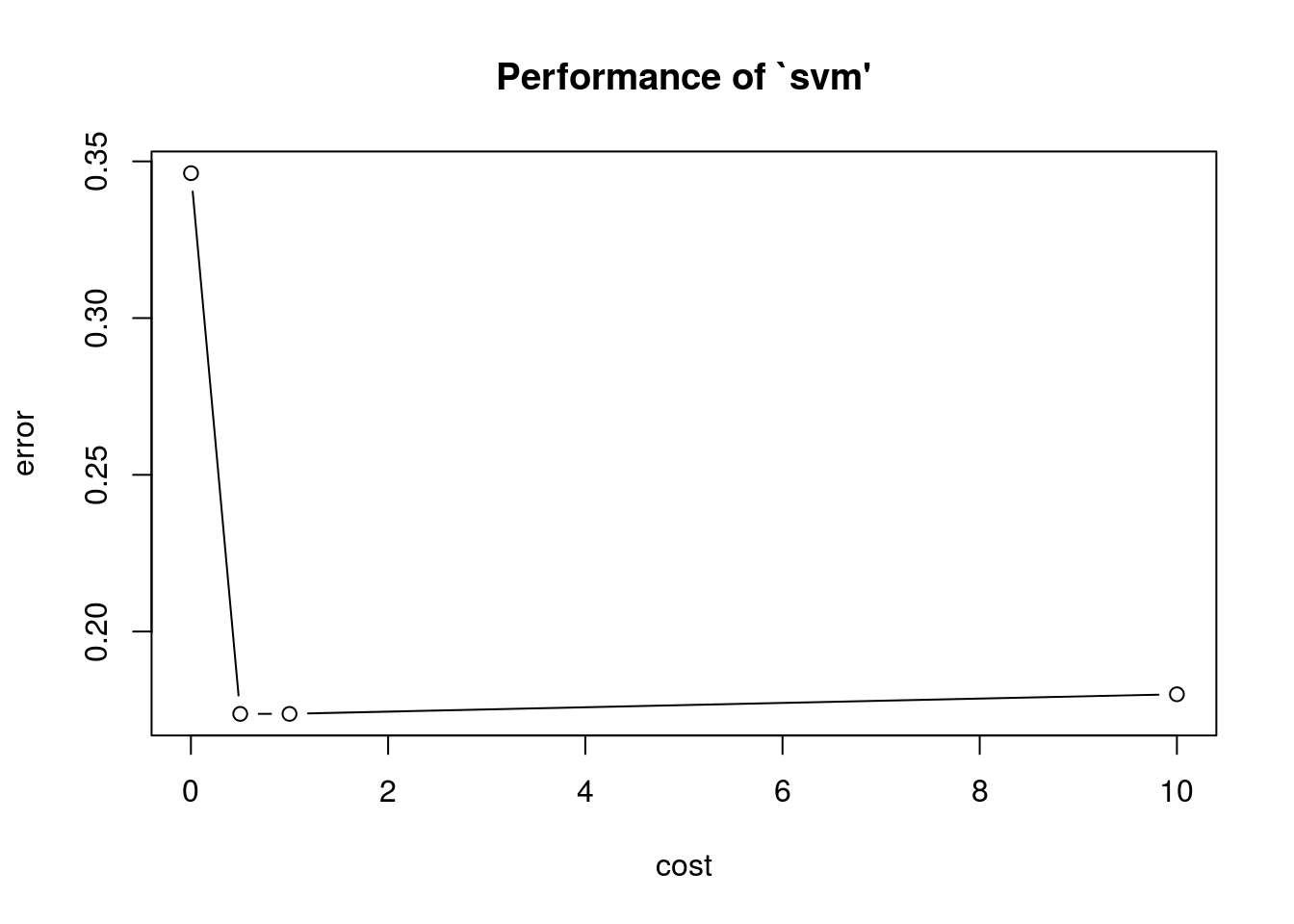

svm.tune$best.parameters

##   cost
## 2  0.5

##-------------------------------------------
## Definindo os melhor classificador nas validações cruzadas
c1l <- svm(Purchase ~ ., kernel = "linear", data = OJ.tr,
           cost = 0.5, probability = TRUE)

## Resumo do classificador
summary(c1l)

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "linear", 
##     cost = 0.5, probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  linear 
##        cost:  0.5 
##       gamma:  0.05555556 
## 
## Number of Support Vectors:  332
## 
##  ( 166 166 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  CH MM

## Gráficos condicionais das fronteiras de classificação
##     Cuidado! Os valores das demais covariáveis utilizadas para
##     classificação são definidas como 0. Isso pode ser alterado pelo
##     argumento slice()
plot(c1l, OJ.tr, WeekofPurchase ~ LoyalCH)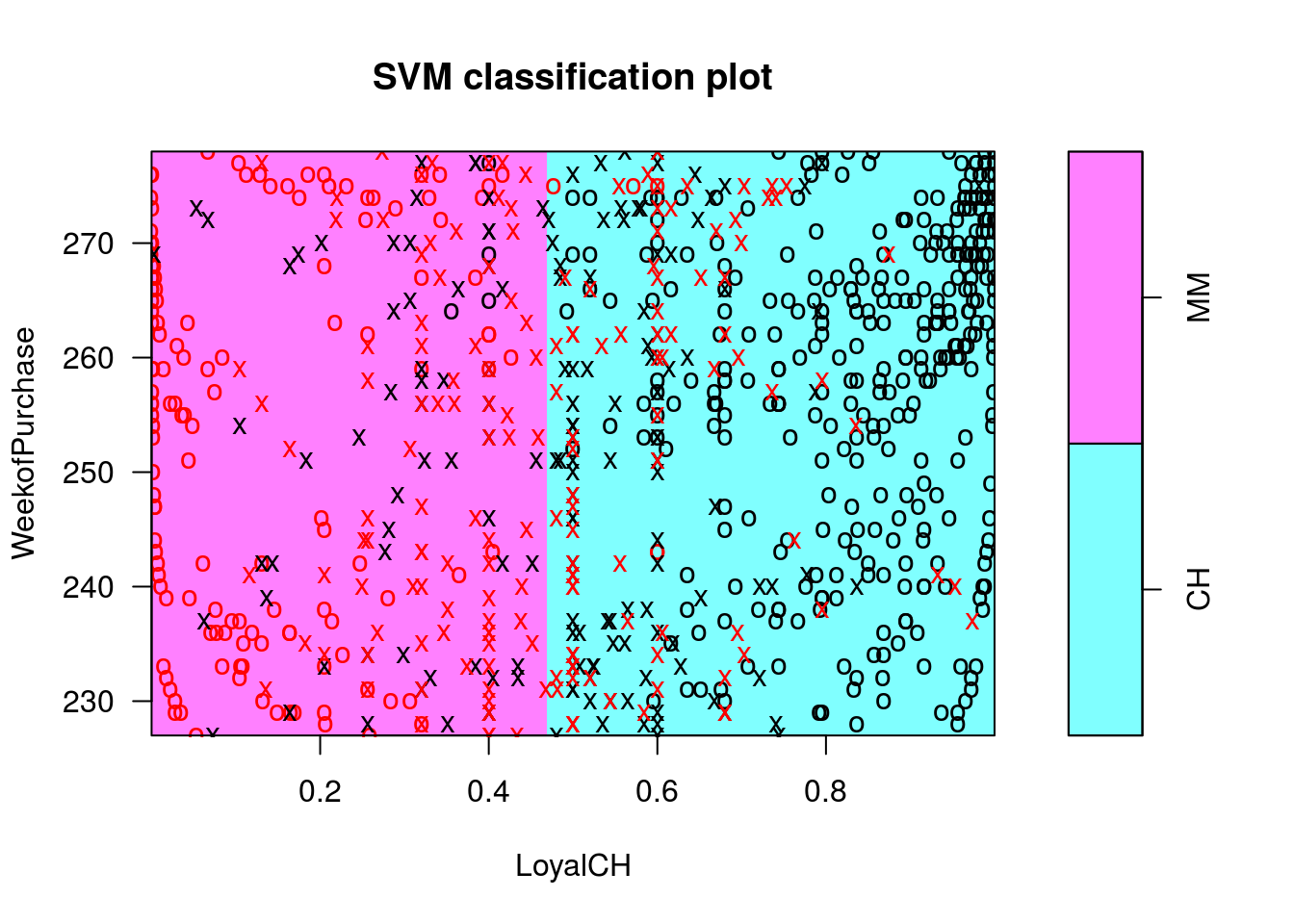

## Tabela de classificação no treino
pred.tr1l <- predict(c1l, newdata = OJ.tr, probability = TRUE)
table(pred.tr1l, OJ.tr$Purchase)

##          
## pred.tr1l  CH  MM
##        CH 443  80
##        MM  54 223

## Tabela de classificação no teste
pred.te1l <- predict(c1l, newdata = OJ.te, probability = TRUE)
table(pred.te1l, OJ.te$Purchase)

##          
## pred.te1l  CH  MM
##        CH 136  21
##        MM  20  93

## Probabilidades associadas as decisões
probs.tr1l <- attr(pred.tr1l, "probabilities")[, 2]
probs.te1l <- attr(pred.te1l, "probabilities")[, 2]

## Curvas ROC
par(mfrow = c(1, 2))
roc.te1l <- ROC(test = probs.tr1l, stat = OJ.tr$Purchase, plot = "ROC")
roc.tr1l <- ROC(test = probs.te1l, stat = OJ.te$Purchase, plot = "ROC")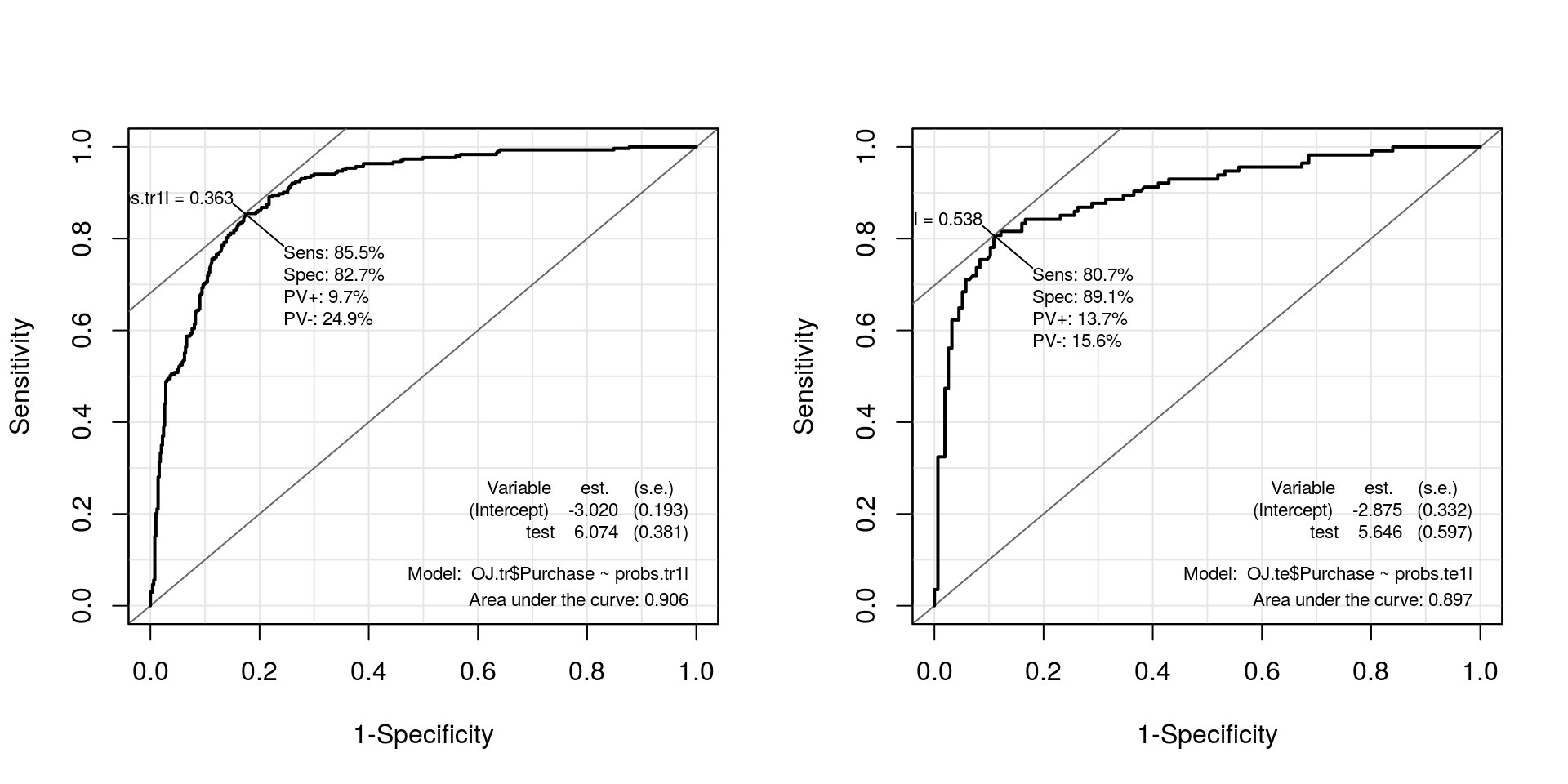

##----------------------------------------------------------------------
## Comparando via AUC, Sensibilidade, Especificidade, Negativo/Positivo,
## Positivo/Negativo e Pontos de Corte respectivamente.
models.linear <- list("c0l.treino" = roc.tr0l, "c1l.treino" = roc.tr1l,
                      "c0l.teste" = roc.te0l, "c1l.teste" = roc.te1l)

## Armazenando o classificador de melhor desempenho
models.final <- list("linear" = roc.te0l)

kable(compareROC(models.linear), align = c("c", "c", "c", "c"))

	c0l.treino	c1l.treino	c0l.teste	c1l.teste
sens	0.8158	0.807	0.8515	0.8548
spec	0.8782	0.891	0.831	0.827
pvp	0.1329	0.1366	0.0983	0.0967
pvn	0.1696	0.156	0.2456	0.2493
prob	0.5	0.5375	0.3741	0.3634
AUC	0.8975	0.897	0.9064	0.9061

SVM kernel polinomial

\[ K(x_i, x_k) = (c_0 + \gamma \left \langle x_i, \, x_k \right \rangle)^d \]

##----------------------------------------------------------------------
##    kernel = polinomial default
(c0p <- svm(Purchase ~ ., kernel = "polynomial", data = OJ.tr,
            probability = TRUE))

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "polynomial", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  polynomial 
##        cost:  1 
##      degree:  3 
##       gamma:  0.05555556 
##      coef.0:  0 
## 
## Number of Support Vectors:  418

## Resumo do modelo
summary(c0p)

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "polynomial", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  polynomial 
##        cost:  1 
##      degree:  3 
##       gamma:  0.05555556 
##      coef.0:  0 
## 
## Number of Support Vectors:  418
## 
##  ( 210 208 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  CH MM

## Classificação dos dados de teste
pred.te0p <- predict(c0p, newdata = OJ.te, probability = TRUE)
probs.te0p <- attr(pred.te0p, "probabilities")[, 2]
roc.te0p <- ROC(test = probs.te0p, stat = OJ.te$Purchase, plot = "ROC")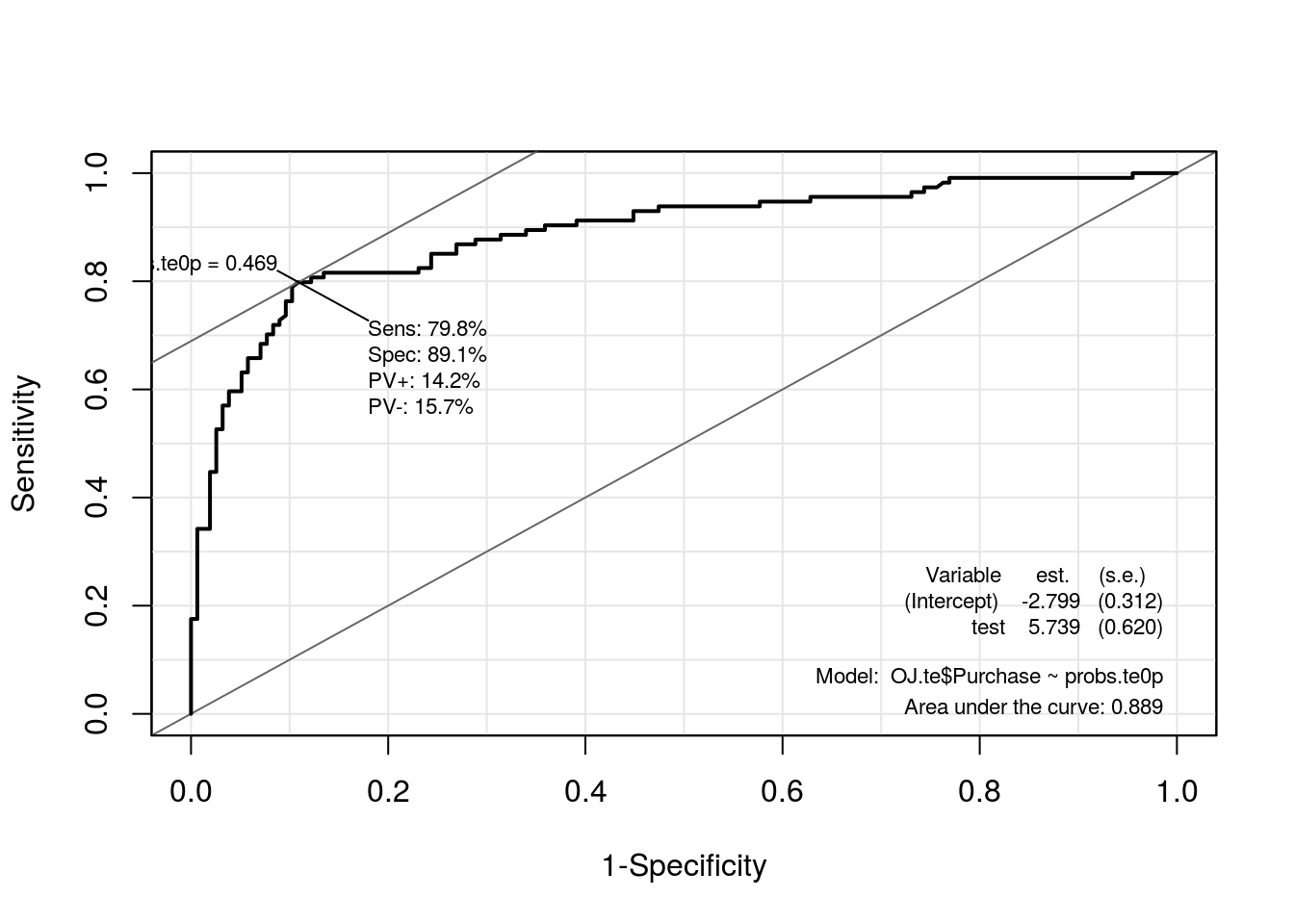

## Tuning dos parâmetros (um pouco, talvez bastante, demorado)
set.seed(2016)
(svm.tune <- tune(svm, Purchase ~ ., data = OJ.tr,
                  kernel = "polynomial",
                  ranges = list(
                      cost = c(0.01, 1, 10),
                      gamma = c(0.01, 1/ncol(OJ), 0.1),
                      coef0 = c(-1, 0, 1),
                      degree = c(2, 3, 4, 5)
                      )))

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost gamma coef0 degree
##     1  0.01     1      2
## 
## - best performance: 0.175

summary(svm.tune)

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost gamma coef0 degree
##     1  0.01     1      2
## 
## - best performance: 0.175 
## 
## - Detailed performance results:
##      cost      gamma coef0 degree   error dispersion
## 1    0.01 0.01000000    -1      2 0.37875 0.04678927
## 2    1.00 0.01000000    -1      2 0.66125 0.04875178
## 3   10.00 0.01000000    -1      2 0.65750 0.05041494
## 4    0.01 0.05555556    -1      2 0.52625 0.04267529
## 5    1.00 0.05555556    -1      2 0.63250 0.04533824
## 6   10.00 0.05555556    -1      2 0.63000 0.04647281
## 7    0.01 0.10000000    -1      2 0.59750 0.02934469
## 8    1.00 0.10000000    -1      2 0.66000 0.03899786
## 9   10.00 0.10000000    -1      2 0.65625 0.03919768
## 10   0.01 0.01000000     0      2 0.37875 0.04678927
## 11   1.00 0.01000000     0      2 0.35500 0.04216370
## 12  10.00 0.01000000     0      2 0.22000 0.02513851
## 13   0.01 0.05555556     0      2 0.37875 0.04678927
## 14   1.00 0.05555556     0      2 0.19375 0.02224391
## 15  10.00 0.05555556     0      2 0.17625 0.02461509
## 16   0.01 0.10000000     0      2 0.35500 0.04216370
## 17   1.00 0.10000000     0      2 0.19125 0.02285978
## 18  10.00 0.10000000     0      2 0.18375 0.02285978
## 19   0.01 0.01000000     1      2 0.37875 0.04678927
## 20   1.00 0.01000000     1      2 0.17500 0.02700309
## 21  10.00 0.01000000     1      2 0.17750 0.02486072
## 22   0.01 0.05555556     1      2 0.30750 0.04297932
## 23   1.00 0.05555556     1      2 0.18250 0.02220485
## 24  10.00 0.05555556     1      2 0.18750 0.02886751
## 25   0.01 0.10000000     1      2 0.20875 0.02889757
## 26   1.00 0.10000000     1      2 0.17875 0.02360703
## 27  10.00 0.10000000     1      2 0.18375 0.03175973
## 28   0.01 0.01000000    -1      3 0.37875 0.04678927
## 29   1.00 0.01000000    -1      3 0.26000 0.03987829
## 30  10.00 0.01000000    -1      3 0.26875 0.07643307
## 31   0.01 0.05555556    -1      3 0.26000 0.04923018
## 32   1.00 0.05555556    -1      3 0.34625 0.04528076
## 33  10.00 0.05555556    -1      3 0.31875 0.04535738
## 34   0.01 0.10000000    -1      3 0.29500 0.05688683
## 35   1.00 0.10000000    -1      3 0.36125 0.03793727
## 36  10.00 0.10000000    -1      3 0.35875 0.04641674
## 37   0.01 0.01000000     0      3 0.37875 0.04678927
## 38   1.00 0.01000000     0      3 0.36625 0.04641674
## 39  10.00 0.01000000     0      3 0.31500 0.02486072
## 40   0.01 0.05555556     0      3 0.36500 0.04816061
## 41   1.00 0.05555556     0      3 0.18750 0.03385016
## 42  10.00 0.05555556     0      3 0.20375 0.02766993
## 43   0.01 0.10000000     0      3 0.31500 0.02486072
## 44   1.00 0.10000000     0      3 0.20500 0.03593976
## 45  10.00 0.10000000     0      3 0.20375 0.04291869
## 46   0.01 0.01000000     1      3 0.37875 0.04678927
## 47   1.00 0.01000000     1      3 0.18000 0.01881932
## 48  10.00 0.01000000     1      3 0.17875 0.03007514
## 49   0.01 0.05555556     1      3 0.20875 0.03007514
## 50   1.00 0.05555556     1      3 0.18500 0.02622022
## 51  10.00 0.05555556     1      3 0.19000 0.02874698
## 52   0.01 0.10000000     1      3 0.18625 0.02729087
## 53   1.00 0.10000000     1      3 0.18750 0.02568506
## 54  10.00 0.10000000     1      3 0.20250 0.03717451
## 55   0.01 0.01000000    -1      4 0.41375 0.03972562
## 56   1.00 0.01000000    -1      4 0.64375 0.05376453
## 57  10.00 0.01000000    -1      4 0.64500 0.05309844
## 58   0.01 0.05555556    -1      4 0.60875 0.04678927
## 59   1.00 0.05555556    -1      4 0.62000 0.04684490
## 60  10.00 0.05555556    -1      4 0.62000 0.04684490
## 61   0.01 0.10000000    -1      4 0.63750 0.03996526
## 62   1.00 0.10000000    -1      4 0.64750 0.04401704
## 63  10.00 0.10000000    -1      4 0.64750 0.04401704
## 64   0.01 0.01000000     0      4 0.37875 0.04678927
## 65   1.00 0.01000000     0      4 0.37875 0.04678927
## 66  10.00 0.01000000     0      4 0.36500 0.04816061
## 67   0.01 0.05555556     0      4 0.36500 0.04816061
## 68   1.00 0.05555556     0      4 0.24000 0.02486072
## 69  10.00 0.05555556     0      4 0.21000 0.03374743
## 70   0.01 0.10000000     0      4 0.31625 0.02766993
## 71   1.00 0.10000000     0      4 0.21250 0.03584302
## 72  10.00 0.10000000     0      4 0.19500 0.03593976
## 73   0.01 0.01000000     1      4 0.37875 0.04678927
## 74   1.00 0.01000000     1      4 0.18000 0.02371708
## 75  10.00 0.01000000     1      4 0.17875 0.02503470
## 76   0.01 0.05555556     1      4 0.19125 0.03120831
## 77   1.00 0.05555556     1      4 0.18750 0.02700309
## 78  10.00 0.05555556     1      4 0.19375 0.03963812
## 79   0.01 0.10000000     1      4 0.18375 0.01868043
## 80   1.00 0.10000000     1      4 0.18875 0.03251602
## 81  10.00 0.10000000     1      4 0.21625 0.04411554
## 82   0.01 0.01000000    -1      5 0.37875 0.04678927
## 83   1.00 0.01000000    -1      5 0.32375 0.05015601
## 84  10.00 0.01000000    -1      5 0.31375 0.04267529
## 85   0.01 0.05555556    -1      5 0.32250 0.04440971
## 86   1.00 0.05555556    -1      5 0.33875 0.04619178
## 87  10.00 0.05555556    -1      5 0.35500 0.04901814
## 88   0.01 0.10000000    -1      5 0.38375 0.04641674
## 89   1.00 0.10000000    -1      5 0.38250 0.02958040
## 90  10.00 0.10000000    -1      5 0.38375 0.03007514
## 91   0.01 0.01000000     0      5 0.37875 0.04678927
## 92   1.00 0.01000000     0      5 0.37875 0.04678927
## 93  10.00 0.01000000     0      5 0.36500 0.04816061
## 94   0.01 0.05555556     0      5 0.36375 0.04730589
## 95   1.00 0.05555556     0      5 0.24125 0.03120831
## 96  10.00 0.05555556     0      5 0.21125 0.03458584
## 97   0.01 0.10000000     0      5 0.30750 0.02220485
## 98   1.00 0.10000000     0      5 0.20125 0.03793727
## 99  10.00 0.10000000     0      5 0.21250 0.03486083
## 100  0.01 0.01000000     1      5 0.36500 0.04556741
## 101  1.00 0.01000000     1      5 0.17875 0.02433134
## 102 10.00 0.01000000     1      5 0.18500 0.02751262
## 103  0.01 0.05555556     1      5 0.18875 0.02531057
## 104  1.00 0.05555556     1      5 0.18375 0.03064696
## 105 10.00 0.05555556     1      5 0.19875 0.04505013
## 106  0.01 0.10000000     1      5 0.18625 0.02598744
## 107  1.00 0.10000000     1      5 0.19500 0.04456581
## 108 10.00 0.10000000     1      5 0.22000 0.02513851

svm.tune$best.parameters

##    cost gamma coef0 degree
## 20    1  0.01     1      2

##-------------------------------------------
## Definindo os melhor classificador com base nas validações cruzadas
c1p <- svm(Purchase ~ ., kernel = "polynomial", data = OJ.tr,
           cost = 10, gamma = 0.01, coef0 = 1, degree = 2,
           probability = TRUE)

## Resumo do modelo
summary(c1p)

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "polynomial", 
##     cost = 10, gamma = 0.01, coef0 = 1, degree = 2, probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  polynomial 
##        cost:  10 
##      degree:  2 
##       gamma:  0.01 
##      coef.0:  1 
## 
## Number of Support Vectors:  331
## 
##  ( 165 166 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  CH MM

plot(c1p, OJ.tr, WeekofPurchase ~ LoyalCH)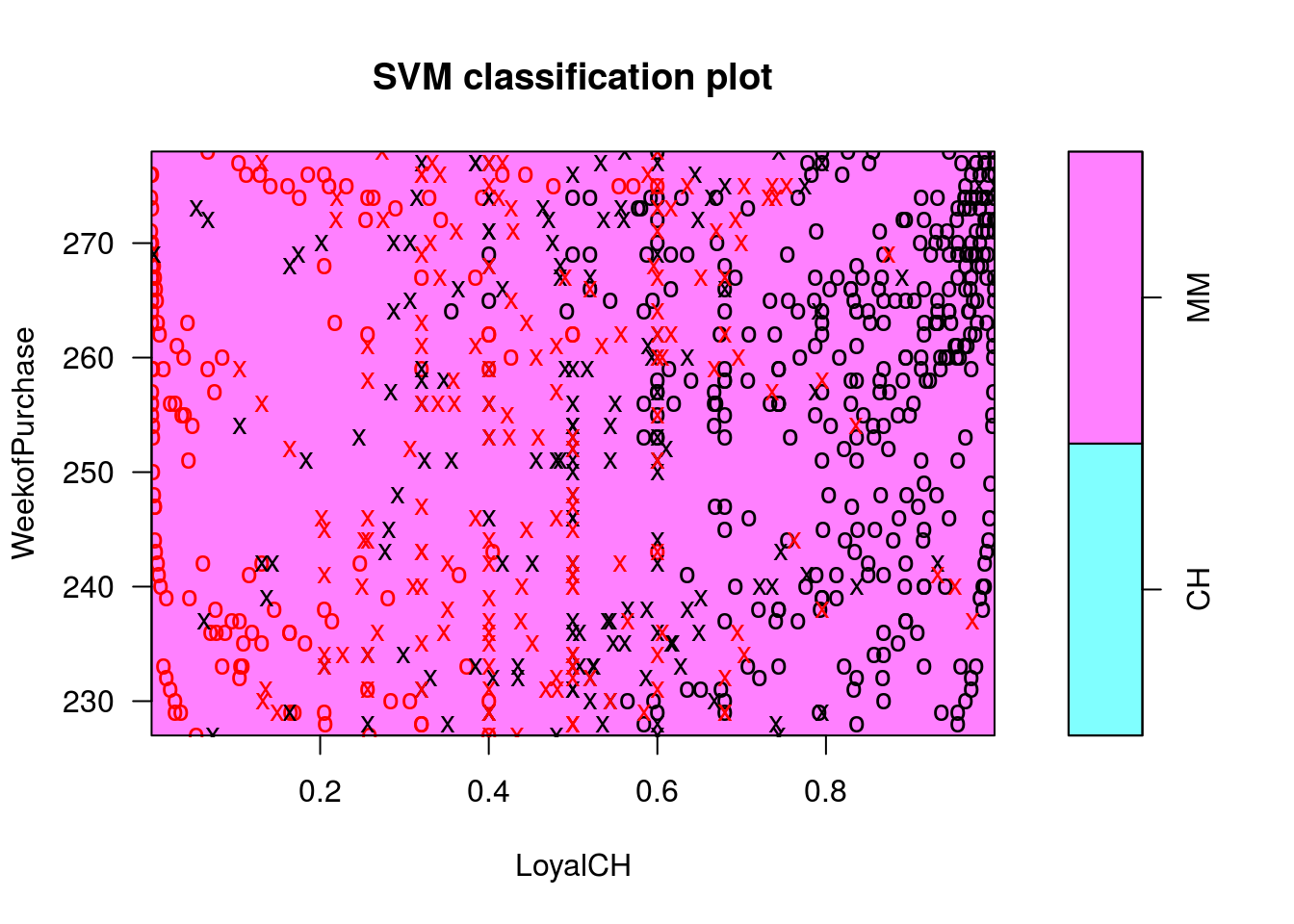

## Classificação dos dados de teste
pred.te1p <- predict(c1p, newdata = OJ.te, probability = TRUE)
probs.te1p <- attr(pred.te1p, "probabilities")[, 2]
roc.te1p <- ROC(test = probs.te1p, stat = OJ.te$Purchase, plot = "ROC")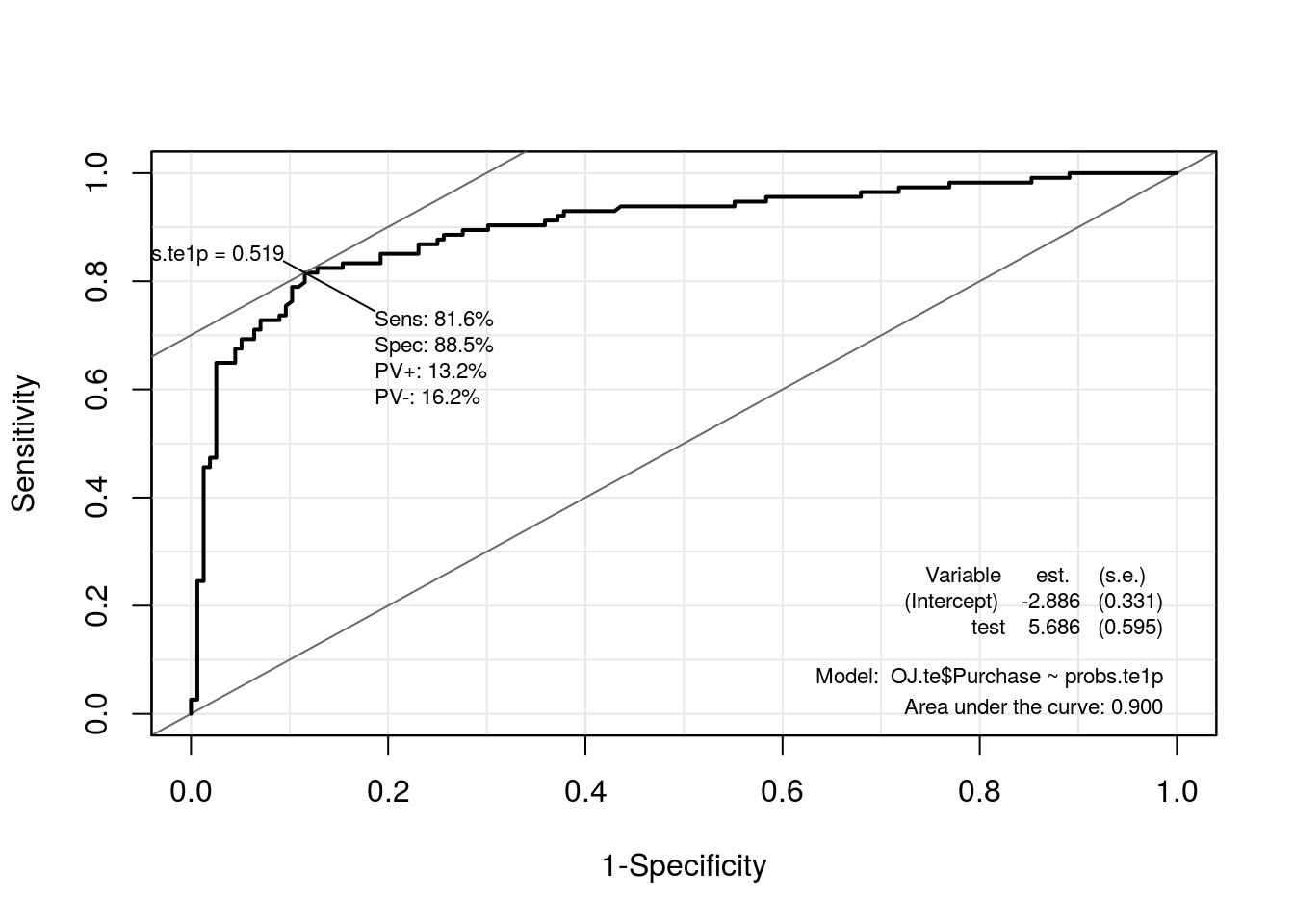

##----------------------------------------------------------------------
## Comparando via AUC, Sensibilidade, Especificidade, Negativo/Positivo,
## Positivo/Negativo e Pontos de Corte respectivamente.
models.poly <- list("c0p.teste" = roc.te0p, "c1p.teste" = roc.te1p)

## Armazenando o classificador de melhor desempenho
models.final$polynomial <- roc.te1p

kable(compareROC(models.poly), align = c("c", "c"))

	c0p.teste	c1p.teste
sens	0.7982	0.8158
spec	0.891	0.8846
pvp	0.142	0.1321
pvn	0.1574	0.1622
prob	0.4689	0.5192
AUC	0.8891	0.9004

SVM kernel radial

\[ K(x_i, x_k) = \exp(-\gamma \left \| x_i, \, x_k \right \|^2 ) \]

##----------------------------------------------------------------------
##    kernel = radial basis
(c0r <- svm(Purchase ~ ., kernel = "radial", data = OJ.tr,
            probability = TRUE))

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "radial", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  radial 
##        cost:  1 
##       gamma:  0.05555556 
## 
## Number of Support Vectors:  373

## Resumo do modelo
summary(c0r)

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "radial", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  radial 
##        cost:  1 
##       gamma:  0.05555556 
## 
## Number of Support Vectors:  373
## 
##  ( 187 186 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  CH MM

## Classificação dos dados de teste
pred.te0r <- predict(c0r, newdata = OJ.te, probability = TRUE)
probs.te0r <- attr(pred.te0r, "probabilities")[, 2]
roc.te0r <- ROC(test = probs.te0r, stat = OJ.te$Purchase, plot = "ROC")

## Tuning dos parâmetros (um pouco demorado)
set.seed(2016)
(svm.tune <- tune(svm, Purchase ~ ., data = OJ.tr,
                  kernel = "radial",
                  ranges = list(
                      cost = c(0.01, 1, 10),
                      gamma = c(0.001, 0.01, 1/ncol(OJ), 0.1, 0.5, 1)
                  )))

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost      gamma
##     1 0.05555556
## 
## - best performance: 0.16625

summary(svm.tune)

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost      gamma
##     1 0.05555556
## 
## - best performance: 0.16625 
## 
## - Detailed performance results:
##     cost      gamma   error dispersion
## 1   0.01 0.00100000 0.37875 0.04678927
## 2   1.00 0.00100000 0.20375 0.03537988
## 3  10.00 0.00100000 0.18250 0.03238227
## 4   0.01 0.01000000 0.37875 0.04678927
## 5   1.00 0.01000000 0.18125 0.01792151
## 6  10.00 0.01000000 0.18125 0.02144923
## 7   0.01 0.05555556 0.37875 0.04678927
## 8   1.00 0.05555556 0.16625 0.02045490
## 9  10.00 0.05555556 0.18750 0.02568506
## 10  0.01 0.10000000 0.37875 0.04678927
## 11  1.00 0.10000000 0.17625 0.02461509
## 12 10.00 0.10000000 0.19000 0.02486072
## 13  0.01 0.50000000 0.37875 0.04678927
## 14  1.00 0.50000000 0.20125 0.03606033
## 15 10.00 0.50000000 0.20875 0.04752558
## 16  0.01 1.00000000 0.37875 0.04678927
## 17  1.00 1.00000000 0.20625 0.03019037
## 18 10.00 1.00000000 0.22125 0.04528076

svm.tune$best.parameters

##   cost      gamma
## 8    1 0.05555556

## Resumo do modelo
plot(c0r, OJ.tr, WeekofPurchase ~ LoyalCH)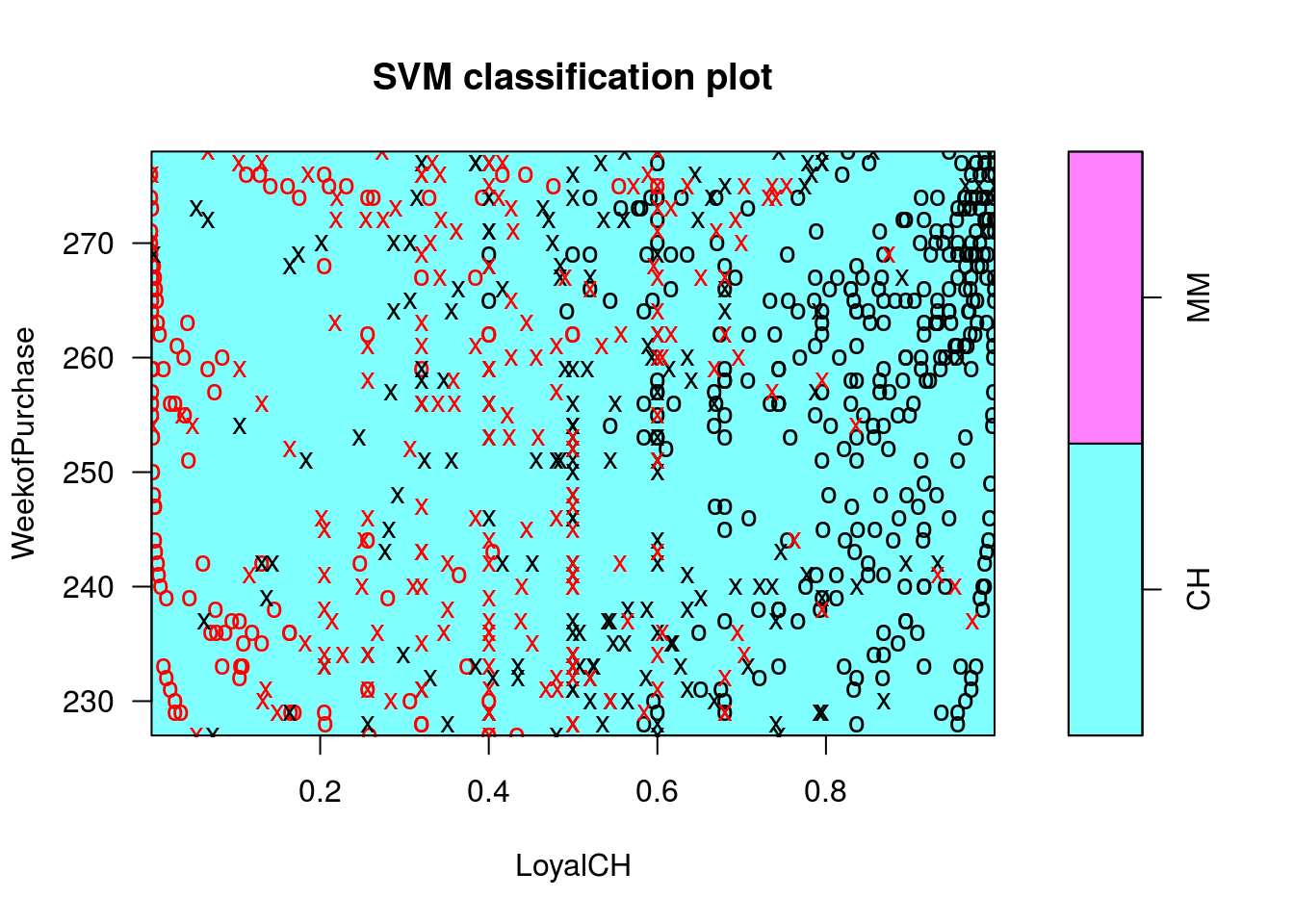

## Armazenando o classificador de melhor desempenho
models.final$radial <- roc.te0r

SVM kernel sigmoid

\[ K(x_i, x_k) = \tanh(c_0 + \gamma \left \langle x_i, \, x_k \right \rangle ) \]

##----------------------------------------------------------------------
##    kernel = sigmoid default
(c0s <- svm(Purchase ~ ., kernel = "sigmoid", data = OJ.tr,
            probability = TRUE))

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "sigmoid", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  sigmoid 
##        cost:  1 
##       gamma:  0.05555556 
##      coef.0:  0 
## 
## Number of Support Vectors:  309

## Resumo do modelo
summary(c0s)

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "sigmoid", 
##     probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  sigmoid 
##        cost:  1 
##       gamma:  0.05555556 
##      coef.0:  0 
## 
## Number of Support Vectors:  309
## 
##  ( 153 156 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  CH MM

## Classificação dos dados de teste
pred.te0s <- predict(c0s, newdata = OJ.te, probability = TRUE)
probs.te0s <- attr(pred.te0s, "probabilities")[, 2]
roc.te0s <- ROC(test = probs.te0s, stat = OJ.te$Purchase, plot = "ROC")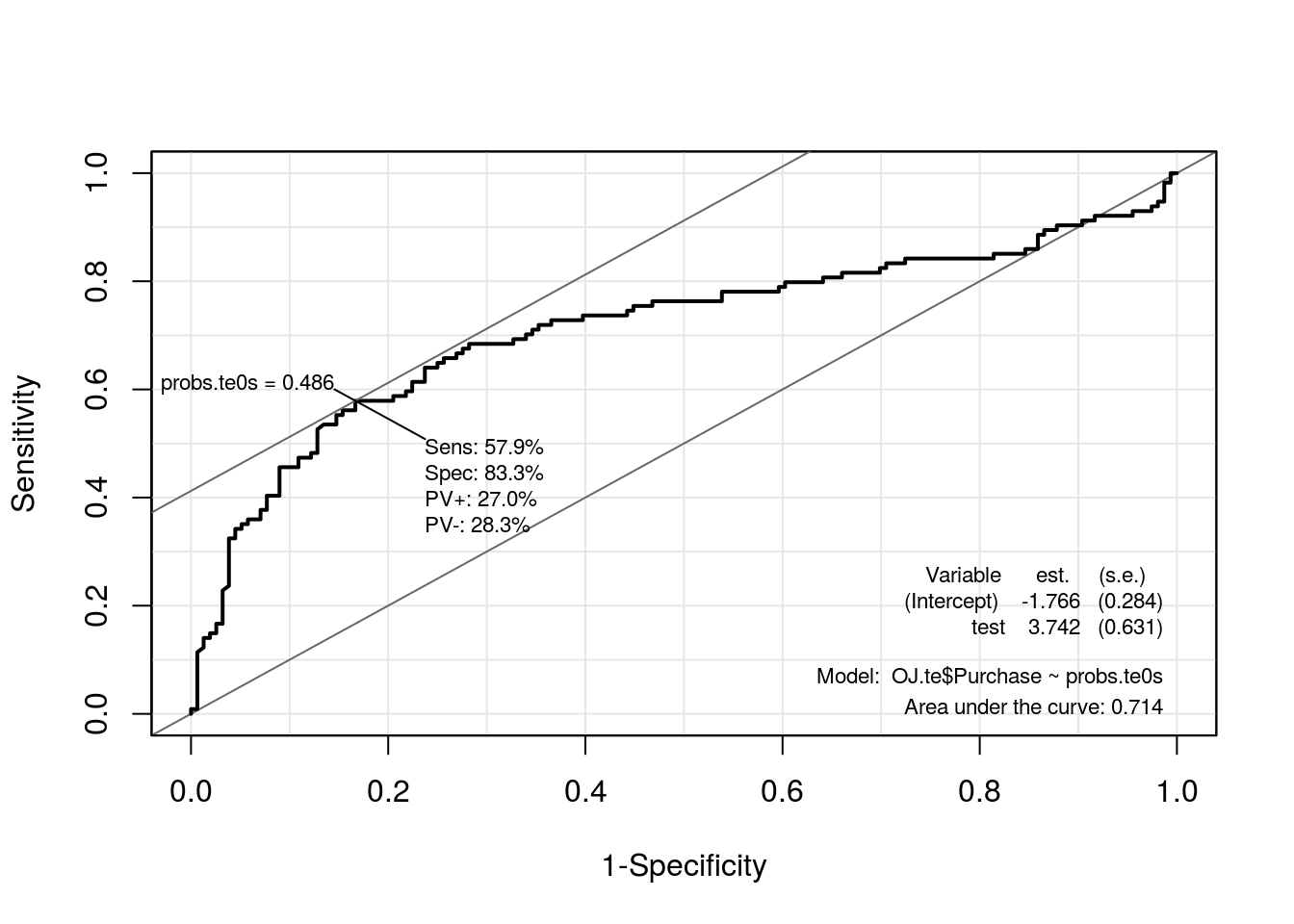

## Tuning dos parâmetros (um pouco demorado)
set.seed(2016)
(svm.tune <- tune(svm, Purchase ~ ., data = OJ.tr,
                  kernel = "sigmoid",
                  ranges = list(
                      cost = c(0.01, 1, 10),
                      gamma = c(0.001, 0.01, 1/ncol(OJ), 0.1, 0.5, 1),
                      coef0 = c(-1, 0, 1)
                  )))

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost gamma coef0
##    10  0.01     0
## 
## - best performance: 0.17125

summary(svm.tune)

## 
## Parameter tuning of 'svm':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  cost gamma coef0
##    10  0.01     0
## 
## - best performance: 0.17125 
## 
## - Detailed performance results:
##     cost      gamma coef0   error dispersion
## 1   0.01 0.00100000    -1 0.37875 0.04678927
## 2   1.00 0.00100000    -1 0.37875 0.04678927
## 3  10.00 0.00100000    -1 0.17875 0.03175973
## 4   0.01 0.01000000    -1 0.37875 0.04678927
## 5   1.00 0.01000000    -1 0.17875 0.03586723
## 6  10.00 0.01000000    -1 0.17750 0.02415229
## 7   0.01 0.05555556    -1 0.37875 0.04678927
## 8   1.00 0.05555556    -1 0.18500 0.03987829
## 9  10.00 0.05555556    -1 0.21125 0.03197764
## 10  0.01 0.10000000    -1 0.37875 0.04678927
## 11  1.00 0.10000000    -1 0.26500 0.06089609
## 12 10.00 0.10000000    -1 0.28750 0.04750731
## 13  0.01 0.50000000    -1 0.30500 0.06697844
## 14  1.00 0.50000000    -1 0.39250 0.07997395
## 15 10.00 0.50000000    -1 0.39625 0.08313518
## 16  0.01 1.00000000    -1 0.29625 0.06181570
## 17  1.00 1.00000000    -1 0.39875 0.06386020
## 18 10.00 1.00000000    -1 0.40375 0.06536489
## 19  0.01 0.00100000     0 0.37875 0.04678927
## 20  1.00 0.00100000     0 0.34625 0.05104804
## 21 10.00 0.00100000     0 0.18625 0.03030516
## 22  0.01 0.01000000     0 0.37875 0.04678927
## 23  1.00 0.01000000     0 0.18500 0.02934469
## 24 10.00 0.01000000     0 0.17125 0.02503470
## 25  0.01 0.05555556     0 0.37875 0.04678927
## 26  1.00 0.05555556     0 0.29875 0.04875178
## 27 10.00 0.05555556     0 0.27750 0.06313566
## 28  0.01 0.10000000     0 0.37875 0.04678927
## 29  1.00 0.10000000     0 0.31125 0.06220765
## 30 10.00 0.10000000     0 0.28625 0.04226652
## 31  0.01 0.50000000     0 0.31500 0.05645795
## 32  1.00 0.50000000     0 0.39000 0.05676462
## 33 10.00 0.50000000     0 0.39375 0.05870418
## 34  0.01 1.00000000     0 0.31125 0.05604128
## 35  1.00 1.00000000     0 0.40250 0.05645795
## 36 10.00 1.00000000     0 0.40500 0.06619626
## 37  0.01 0.00100000     1 0.37875 0.04678927
## 38  1.00 0.00100000     1 0.37875 0.04678927
## 39 10.00 0.00100000     1 0.18000 0.03395258
## 40  0.01 0.01000000     1 0.37875 0.04678927
## 41  1.00 0.01000000     1 0.18375 0.03488573
## 42 10.00 0.01000000     1 0.24250 0.04456581
## 43  0.01 0.05555556     1 0.37875 0.04678927
## 44  1.00 0.05555556     1 0.30875 0.04566256
## 45 10.00 0.05555556     1 0.32250 0.04322101
## 46  0.01 0.10000000     1 0.37875 0.04678927
## 47  1.00 0.10000000     1 0.37625 0.03747684
## 48 10.00 0.10000000     1 0.37125 0.03775377
## 49  0.01 0.50000000     1 0.33875 0.05756940
## 50  1.00 0.50000000     1 0.38875 0.06358776
## 51 10.00 0.50000000     1 0.36750 0.04174992
## 52  0.01 1.00000000     1 0.32625 0.05787019
## 53  1.00 1.00000000     1 0.39000 0.05737305
## 54 10.00 1.00000000     1 0.39500 0.05898446

svm.tune$best.parameters

##    cost gamma coef0
## 24   10  0.01     0

##-------------------------------------------
## Definindo os melhor classificador com base nas validações cruzadas
c1s <- svm(Purchase ~ ., kernel = "sigmoid", data = OJ.tr,
           cost = 10, gamma = 0.01, coef0 = 0, probability = TRUE)

## Resumo do modelo
summary(c1s)

## 
## Call:
## svm(formula = Purchase ~ ., data = OJ.tr, kernel = "sigmoid", 
##     cost = 10, gamma = 0.01, coef0 = 0, probability = TRUE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  sigmoid 
##        cost:  10 
##       gamma:  0.01 
##      coef.0:  0 
## 
## Number of Support Vectors:  343
## 
##  ( 173 170 )
## 
## 
## Number of Classes:  2 
## 
## Levels: 
##  CH MM

plot(c1s, OJ.tr, WeekofPurchase ~ LoyalCH)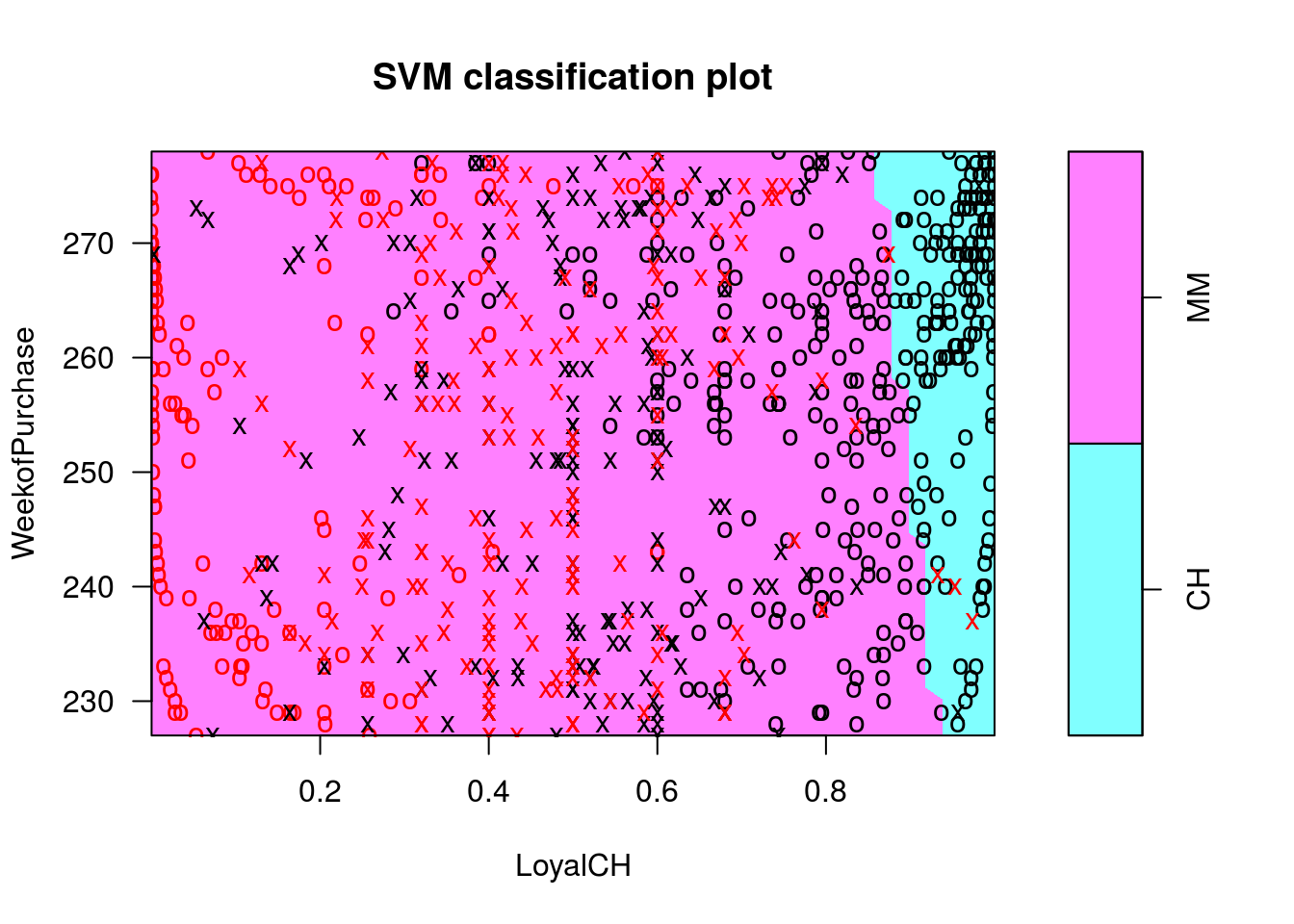

## Classificação dos dados de teste
pred.te1s <- predict(c1s, newdata = OJ.te, probability = TRUE)
probs.te1s <- attr(pred.te1s, "probabilities")[, 2]
roc.te1s <- ROC(test = probs.te1s, stat = OJ.te$Purchase, plot = "ROC")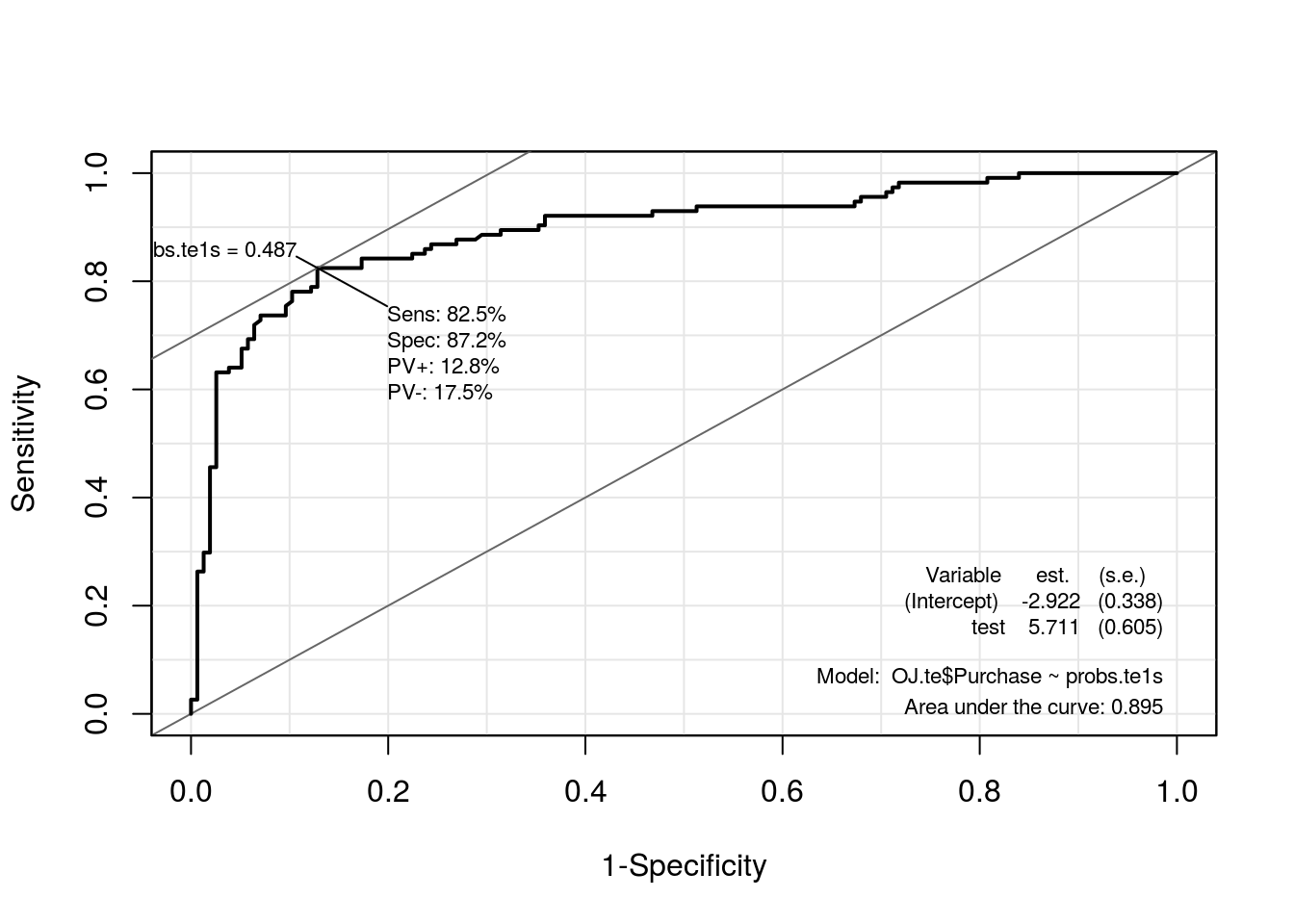

##----------------------------------------------------------------------
## Comparando via AUC, Sensibilidade, Especificidade, Negativo/Positivo,
## Positivo/Negativo e Pontos de Corte respectivamente.
models.sigmoid <- list("c0s.teste" = roc.te0s, "c1s.teste" = roc.te1s)

## Armazenando o classificador de melhor desempenho
models.final$sigmoid <- roc.te1s

kable(compareROC(models.sigmoid), align = c("c", "c"))

	c0s.teste	c1s.teste
sens	0.5789	0.8246
spec	0.8333	0.8718
pvp	0.2697	0.1282
pvn	0.2826	0.1754
prob	0.4862	0.4871
AUC	0.7142	0.8946

Comparação dos ajustes

## Comparação visual
plot(0, 0, xlim = c(0, 1), ylim = c(0, 1), type = "n",
     xlab = "1-Specificity", ylab = "Sensitivity")
abline(v = seq(0, 1, 0.1), h = seq(0, 1, 0.1), col = "gray90")
abline(0, 1, col = "gray40")
##
sapply(1:length(models.final), function(i) {
    with(models.final[[i]],
         points(1 - res[, 2], res[, 1], type = "l", col = i))
})

## [[1]]
## NULL
## 
## [[2]]
## NULL
## 
## [[3]]
## NULL
## 
## [[4]]
## NULL

##
legend(x = 0.7, y = 0.4, lwd = 1,
       bty = "n", col = 1:length(models.final),
       legend = names(models.final))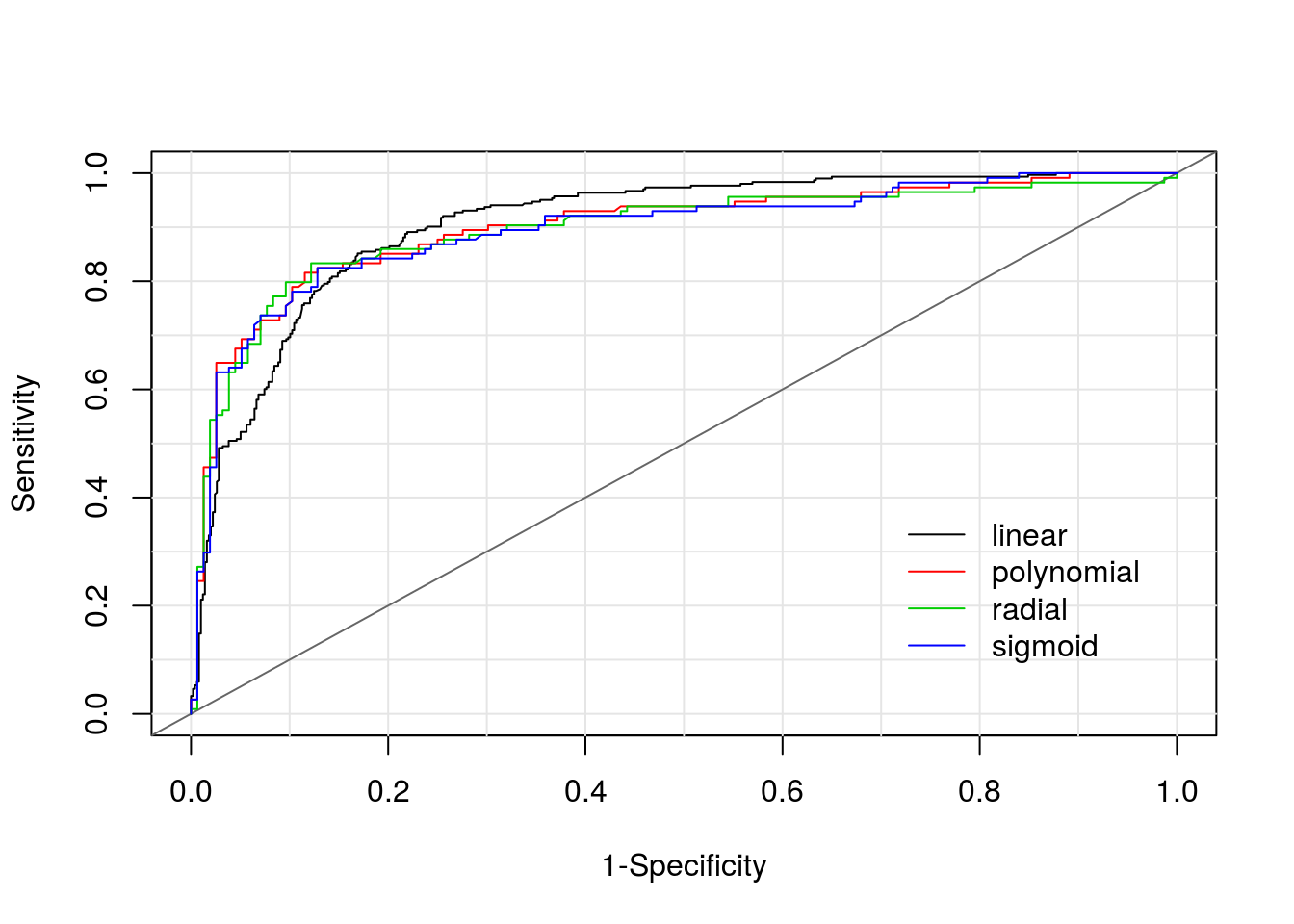

## Comparação das medidas de classificação
kable(compareROC(models.final), align = c("c", "c", "c", "c"))

	linear	polynomial	radial	sigmoid
sens	0.8515	0.8158	0.8333	0.8246
spec	0.831	0.8846	0.8782	0.8718
pvp	0.0983	0.1321	0.1218	0.1282
pvn	0.2456	0.1622	0.1667	0.1754
prob	0.3741	0.5192	0.4915	0.4871
AUC	0.9064	0.9004	0.8954	0.8946

Sabatina

Proponha um classificador baseado em Supporte Vector Machine para classificar a espécie das plantas no conjunto de dados iris do R. Considere ao menos 2 classificadores para comparação via classificação em uma base de teste.

Para particionar os dados em base de treino e teste, pode-se seguir os comandos abaixo.

##======================================================================
## Sabatina
data(iris, package = "datasets")

## Dados balanceados com base na espécie
table(iris$Species)

## 
##     setosa versicolor  virginica 
##         50         50         50

## Utilize como semente seu GRR
set.seed(20124689)
index <- matrix(c(0, 50, 100), ncol = 3, nrow = 30, byrow = TRUE) +
    replicate(3, sample(1:50, 30))

## Particione os dados em dados de treino e dados de teste
iris.tr <- iris[c(index), ]
iris.te <- iris[-c(index), ]

## Dados balanceados para treino também
table(iris.tr$Species)

## 
##     setosa versicolor  virginica 
##         30         30         30

table(iris.te$Species)

## 
##     setosa versicolor  virginica 
##         20         20         20

Informações da sessão R

cat(format(Sys.time(),
           format = "Atualizado em %d de %B de %Y.\n\n"))

## Atualizado em 08 de agosto de 2016.

sessionInfo()

## R version 3.3.1 (2016-06-21)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 14.04.5 LTS
## 
## locale:
##  [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
##  [3] LC_TIME=pt_BR.UTF-8        LC_COLLATE=en_US.UTF-8    
##  [5] LC_MONETARY=pt_BR.UTF-8    LC_MESSAGES=en_US.UTF-8   
##  [7] LC_PAPER=pt_BR.UTF-8       LC_NAME=C                 
##  [9] LC_ADDRESS=C               LC_TELEPHONE=C            
## [11] LC_MEASUREMENT=pt_BR.UTF-8 LC_IDENTIFICATION=C       
## 
## attached base packages:
## [1] parallel  stats     graphics  grDevices utils     datasets  methods  
## [8] base     
## 
## other attached packages:
##  [1] e1071_1.6-7         klaR_0.6-12         Epi_2.0            
##  [4] MASS_7.3-45         glmnet_2.0-5        foreach_1.4.3      
##  [7] Matrix_1.2-6        mboost_2.6-0        stabs_0.5-1        
## [10] knitr_1.12.3        latticeExtra_0.6-28 RColorBrewer_1.1-2 
## [13] lattice_0.20-33    
## 
## loaded via a namespace (and not attached):
##  [1] Rcpp_0.12.5       compiler_3.3.1    formatR_1.3      
##  [4] highr_0.5.1       plyr_1.8.3        class_7.3-14     
##  [7] iterators_1.0.8   tools_3.3.1       digest_0.6.9     
## [10] evaluate_0.9      cmprsk_2.2-7      yaml_2.1.13      
## [13] mvtnorm_1.0-5     coin_1.1-2        stringr_1.0.0    
## [16] combinat_0.0-8    stats4_3.3.1      grid_3.3.1       
## [19] survival_2.39-4   etm_0.6-2         rmarkdown_0.9.6  
## [22] multcomp_1.4-5    TH.data_1.0-7     magrittr_1.5     
## [25] codetools_0.2-14  htmltools_0.3     modeltools_0.2-21
## [28] nnls_1.4          splines_3.3.1     strucchange_1.5-1
## [31] quadprog_1.5-5    sandwich_2.3-4    stringi_1.0-1    
## [34] party_1.0-25      zoo_1.7-13

Machine Learning - Support Vector Machine

Eduardo E. R. Junior - DEST/UFPR

17 de maio de 2016