Machine Learning - Métodos de Classificação Supervisionados
Eduardo E. R. Junior - DEST/UFPR
05 de maio de 2016
Conjunto de dados
Para a aplicação dos métodos de classificação apresentados em sala de aula utilizaremos a conjunto Pima.te e Pima.tr, do pacote MASS do software R. Estes dados se referem a um levantamento realizado pelo Instituto Nacional de Diabetes, Doenças Digestivas e Renais dos Estados Unidados com mulheres do povoado indígena Pima, próximo a Phoenix, Estado do Arizona. Ao todo a base de dados contém o registro de 8 variáveis, contudo nesse trabalho utilizaremos somente as variáveis descritas abaixo.
type:Se a mulher tem ou não diabetes, com base nos critérios da OMS;bmi:índice de massa corporal, calculado como peso\(cdot\)altura\(^{-2}\), sendo o peso e a altura mensurados em quilogramas e metros respectivamente.ped:Diabetes Pedigree Function (DPF), valores que medem a tendência ao desenvolvimento de diabetes com base nas relações genéticas do indivíduo.1
O objetivo neste estudo é classificar as mulheres com e sem diabetes baseando-se no índice de massa corporal e no valor da função DPF. Uma característica destes dados é que eles já estão divididos em, no R, em base a ser utilizada para o treino do método classificador, Pima.tr e base de teste para utilizar o método já calibrado, denominada Pima.te.
Abaixo temos a representação gráfica do conjunto de dados.
library(MASS)
id <- c(rep("treino", nrow(Pima.tr)),
rep("teste", nrow(Pima.te)))
xyplot(bmi ~ ped | id, groups = type,
grid = TRUE,
data = rbind(Pima.tr, Pima.te))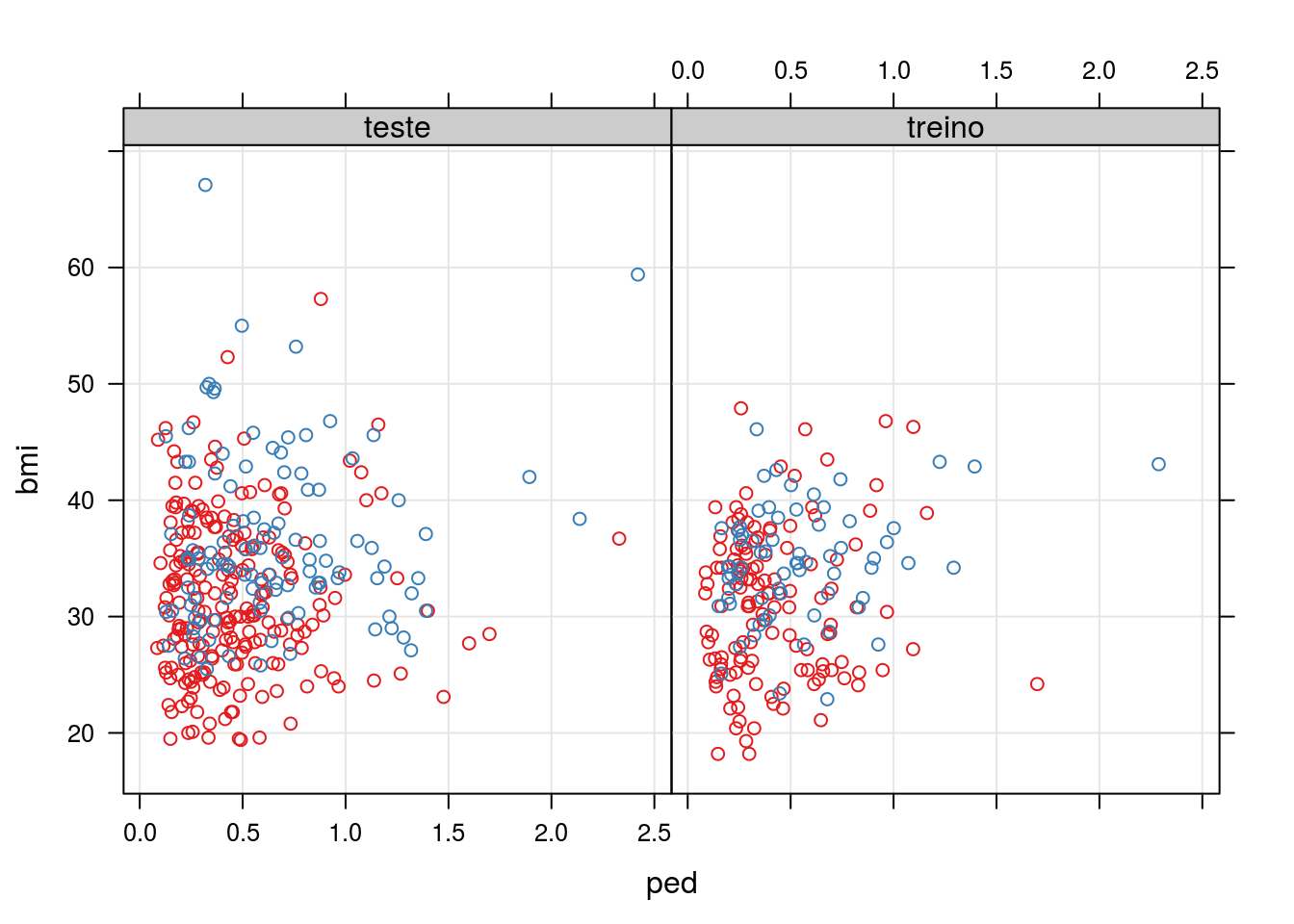
Dados de treino
## Visualizando os dados para antecipar problemas com classificadores
d1 <- densityplot(~bmi, groups = type, grid = TRUE, data = Pima.tr)
d2 <- densityplot(~ped, groups = type, grid = TRUE, data = Pima.tr)
print(d1, split = c(2, 1, 2, 1), more = TRUE)
print(d2, split = c(1, 1, 2, 1), more = FALSE)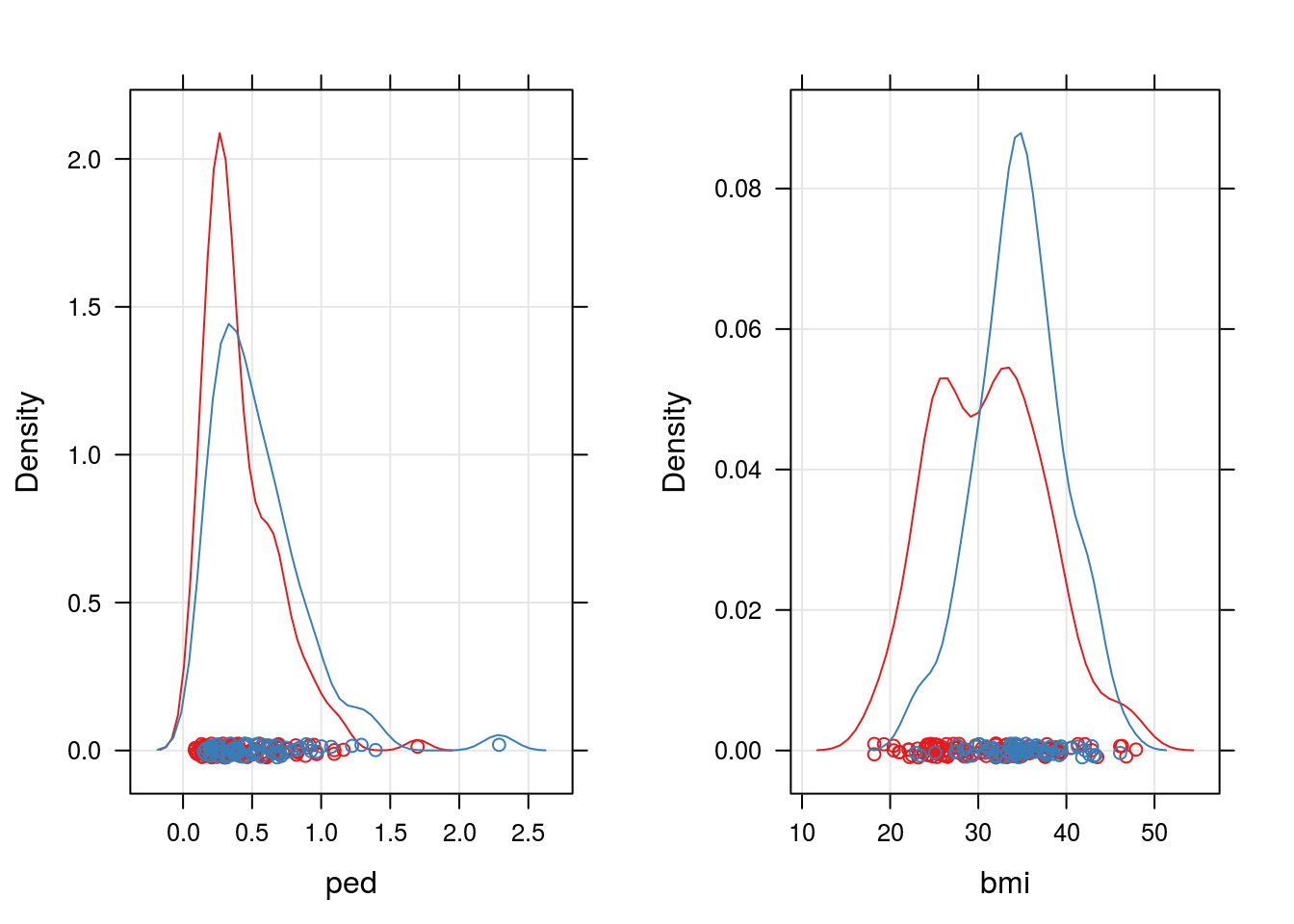
Com base nos gráficos acima já podemos prever uma taxa de classificação não tão elevada, pois as variáveis escolhidas para classificação estão dispostas de forma muito similar.
Métodos de classificação
Modelo logístico
O modelo denominado modelo logístico é um modelo da classe dos modelos lineares generalizados, cujo a distribuição considerada para a relação condicional \(Y \mid X\) é Binomial(\(m\), \(\pi\)) e função de ligação logito (qu dá nome ao modelo). Assim o modelo pode ser escrito da seguinte forma:
\[ \begin{aligned} Y \mid X_i \sim \textrm{Binomial}(m_i, \, \pi_i) \\ \log \left ( \frac{\pi}{ 1 - \pi} \right ) = X\beta \end{aligned} \]
No software R (nativo na instalação, pacote base), temos os framework glm que ajuste modelos de regressão lineares generalizados via minimização da função deviance. Utilizaremos esta função para ajuste do modelo logístico e alternativamente será programado o algoritmo de maximização da log-verossimilhança para exemplicar o método de estimação dos parâmetros. Como são otimizações equivalentes os resultados devem ser iguais.
## Função para estimação de um GLM Binomial (restrito a n = 1)
binomreg <- function(formula, data) {
## Declarando a função de verossimilhança
veross <- function(betas, y, X, log = TRUE) {
eXb <- exp(X %*% betas)
pi <- eXb / (1 + eXb)
ll <- sum(y * log(pi) + (1 - y) * log(1 - pi))
if (!log) ll <- exp(ll)
return(ll)
}
## Definindo as matrizes do modelo
frame <- model.frame(formula, data = data)
y <- model.response(frame)
X <- model.matrix(formula, data)
if(!class(y) %in% c("numeric", "integer")) {
y <- as.integer(y) - 1
}
## Otimizando
opt <- optim(par = rep(0, ncol(X)), veross,
y = y, X = X, method = "BFGS",
control = list(fnscale = -1))
return(opt)
}
##-------------------------------------------
## Utilizando a função no nosso conjunto de dados
## Definindo os preditores lineares
f1 <- type ~ 1
f2 <- type ~ bmi + ped
## Ajustando os modelos com a função descrita
m1 <- binomreg(f1, data = Pima.tr)
m2 <- binomreg(f2, data = Pima.tr)
## Ajustando os modelos com a glm
g1 <- glm(f1, data = Pima.tr, family = binomial)
g2 <- glm(f2, data = Pima.tr, family = binomial)
## Comparando os ajustes
## Log-verossimilhança alcançada
cbind("GLM" = c(logLik(g1), logLik(g2)),
"binomreg" = c(m1$value, m2$value))## GLM binomreg
## [1,] -128.2071 -128.2071
## [2,] -117.5110 -117.5110## Agora os coeficientes estimados
cbind("GLM" = c(coef(g1), coef(g2)),
"binomreg" = c(m1$par, m2$par))## GLM binomreg
## (Intercept) -0.66329422 -0.66329424
## (Intercept) -4.37613317 -4.37517161
## bmi 0.09612468 0.09610259
## ped 1.17601545 1.17561713Verificando agora o poder preditivo (de classificação) do modelo ajustado
library(Epi)
## ROC(form = f2, data = Pima.tr, plot = "ROC")
probs <- predict(g2, type = "response")
ROC(test = probs, stat = Pima.tr$type, plot = "ROC")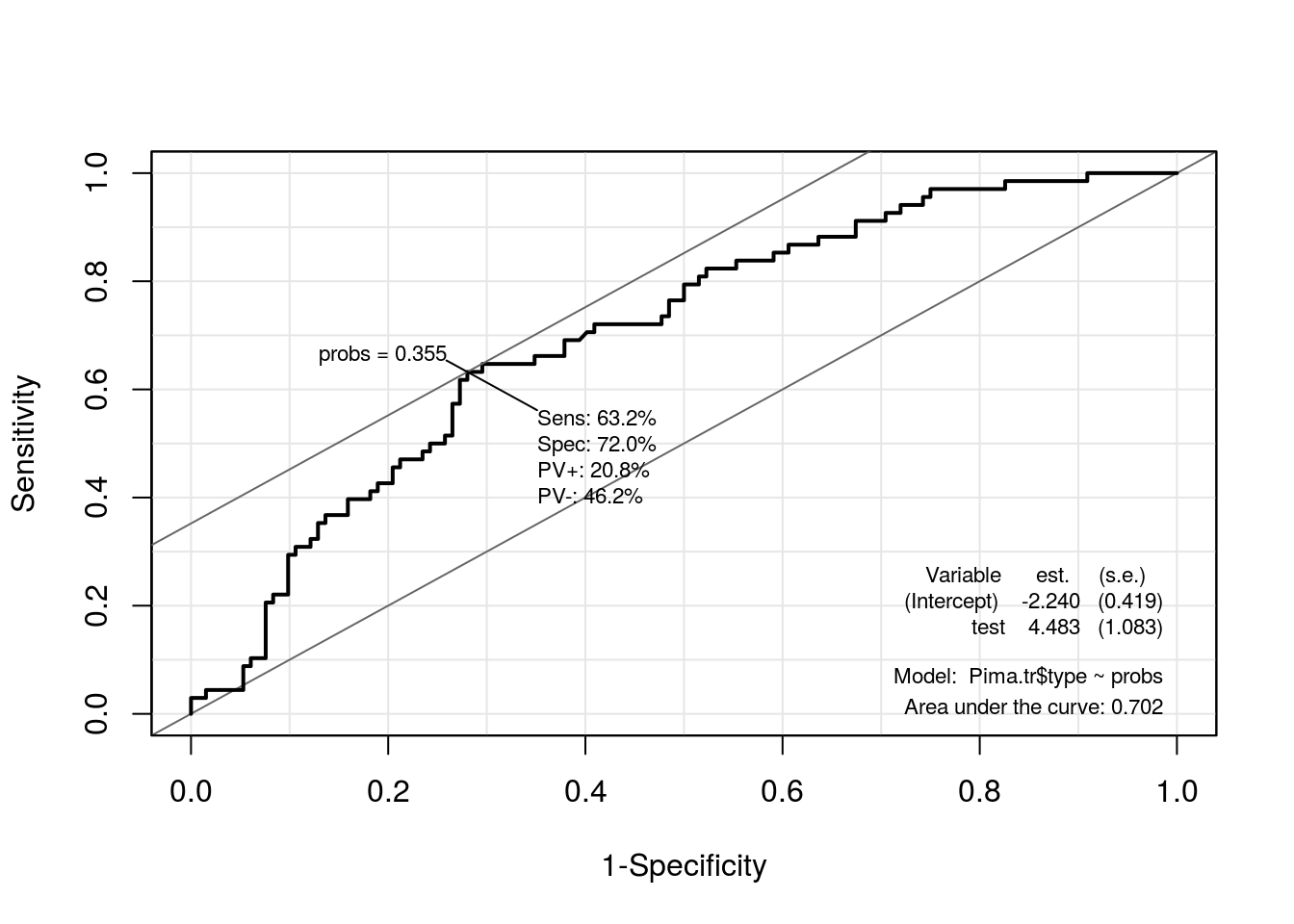
## Realizando a classificação via GLM com ponto de corte ótimo
cg <- ifelse(predict(g2, type = "response") > 0.3553, "Yes", "No")
## Tabela de classificação no treino
(tcg <- table(cg, Pima.tr$type))##
## cg No Yes
## No 95 25
## Yes 37 43## Tabela de classificação no teste
cg <- ifelse(predict(g2, newdata = Pima.te, type = "response") > 0.3553,
"Yes", "No")
table(cg, Pima.te$type)##
## cg No Yes
## No 139 31
## Yes 84 78Discriminante de Fisher
Discriminante Linear
library(MASS)
## Realizando a análise via Discriminante linear
dl <- lda(type ~ ped + bmi, data = Pima.tr)
## Tabela de classificação no treino
(tdl <- table(predict(dl)$class, Pima.tr$type))##
## No Yes
## No 119 51
## Yes 13 17## Tabela de classificação no teste
table(predict(dl, newdata = Pima.te)$class, Pima.te$type)##
## No Yes
## No 195 65
## Yes 28 44Discriminante quadrático
library(MASS)
## Realizando a análise via Discriminante linear
dq <- qda(type ~ ped + bmi, data = Pima.tr)
## Tabela de classificação no treino
(tdq <- table(predict(dq)$class, Pima.tr$type))##
## No Yes
## No 123 55
## Yes 9 13## Tabela de classificação no teste
table(predict(dq, newdata = Pima.te)$class, Pima.te$type)##
## No Yes
## No 204 73
## Yes 19 36Discriminante Regularizado
library(klaR)
## Realizando a análise via Discriminante linear
dr <- rda(type ~ ped + bmi, data = Pima.tr)
## Tabela de classificação no treino
(tdr <- table(predict(dr)$class, Pima.tr$type))##
## No Yes
## No 120 53
## Yes 12 15## Tabela de classificação no teste
table(predict(dr, newdata = Pima.te)$class, Pima.te$type)##
## No Yes
## No 197 68
## Yes 26 41Comparando os métodos
Como comparação de métodos de classificação temos, além das tabelas de predição um gráfico que apresenta, geralmente os valores de especificidade e sensibilidade calculados para um intervalo de pontos de corte considerados na classificação. Este gráfico já fora utilizado na seção Modelo Logístico, onde a utilizamos para encontrar o ponto de corte ótimo de classificação. Aqui como critério de comparação utilizaremos a área abaixo da curva (do inglês Area Under the Curve - AUC), pois quanto maior a área maior a acertividade do método.
par(mfrow = c(2, 2))
## Para o GLM
probs1 <- predict(g2, type = "response")
rcg <- ROC(test = probs1, stat = Pima.tr$type, plot = "ROC")
title("Regressão Logística")
## Para o Discriminante Linear
probs2 <- predict(dl)$posterior[, "Yes"]
rdl <- ROC(test = probs2, stat = Pima.tr$type, plot = "ROC")
title("Discriminante Linear")
## Para o Discriminante Quadrático
probs3 <- predict(dq)$posterior[, "Yes"]
rdq <- ROC(test = probs3, stat = Pima.tr$type, plot = "ROC")
title("Discriminante Quadrático")
## Para o Discriminante Regularizado
probs4 <- predict(dr)$posterior[, "Yes"]
rdr <- ROC(test = probs4, stat = Pima.tr$type, plot = "ROC")
title("Discriminante Regularizado")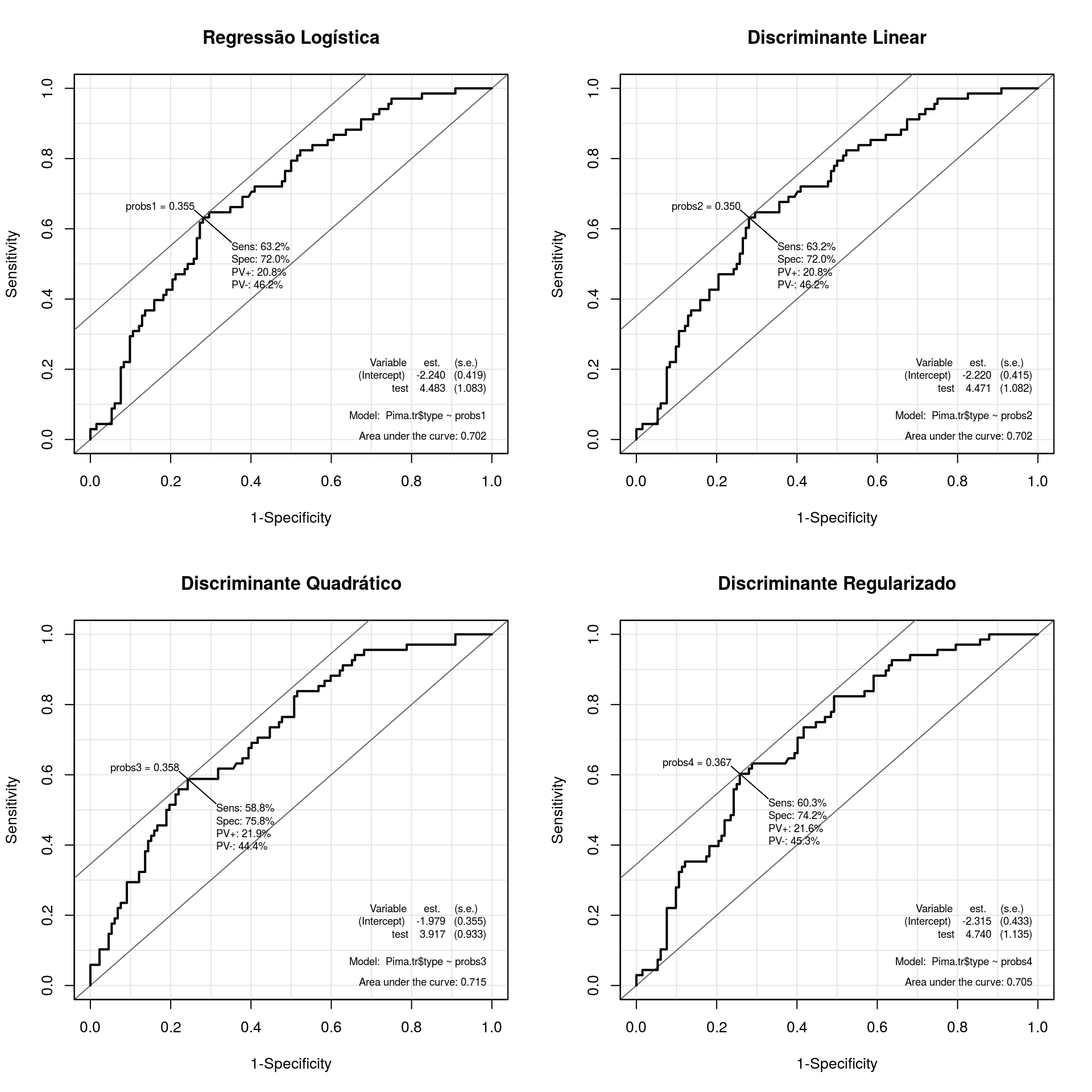
## Comparando via AUC, Sensibilidade, Especificidade, Negativo/Positivo,
## Positivo/Negativo e Pontos de Corte respectivamente.
tableC <- sapply(list(rcg, rdl, rdq, rdr),
FUN = function(roc) {
index <- with(roc$res,
which.max(sens + spec))
round(cbind(roc$res[index, ],
"AUC" = roc$AUC), 4)
})
colnames(tableC) <- c("Reg. Logística", "Discr. Linear",
"Discr. Quadrático", "Discr. Regularizado")
kable(tableC, align = c("c", "c", "c", "c"))| Reg. Logística | Discr. Linear | Discr. Quadrático | Discr. Regularizado | |
|---|---|---|---|---|
| sens | 0.6324 | 0.6324 | 0.5882 | 0.6029 |
| spec | 0.7197 | 0.7197 | 0.7576 | 0.7424 |
| pvp | 0.2083 | 0.2083 | 0.2188 | 0.216 |
| pvn | 0.4625 | 0.4625 | 0.4444 | 0.4533 |
| probs1 | 0.3553 | 0.3503 | 0.3577 | 0.3666 |
| AUC | 0.7023 | 0.7019 | 0.7153 | 0.7049 |
Pelos gráficos e pela tabela acima temos o método de classificação por Discrinante Quadrático de Fisher com um desempenho ligeiramente superior aos demais que se seguem na ordem Regressão Logística e Discriminante Linear com desempenho equivalente e via Discriminante Regularizado com o pior desempenho.
Ressalta-se aqui que não consideramos na análise custos associados a falsos positivos e falsos negativos, ou ainda benefícios à verdadeiros positivos e verdadeiros negativos. Isto pode e deve, quando disponível, ser levado em consideração, neste trabalho todas essas situações tem o peso peso e assim foram calculados os demais resultados (principalmente o ponto de corte de classificação, que leva em conta o ponto que maximiza a especificidade e sensibilidade conjuntamente). Ainda destacamos que, embora nesse caso tenhamos os resultados no conjunto de teste Pima.te, na prática isso não acontece e portanto tentou-se reproduzir uma análise real, onde todos os resultados são retirados do conjunto de treino para, então o método calibrado ser aplicado ao conjunto de treino.
Informações da sessão R
cat(format(Sys.time(),
format = "Atualizado em %d de %B de %Y.\n\n"))## Atualizado em 08 de agosto de 2016.sessionInfo()## R version 3.3.1 (2016-06-21)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 14.04.5 LTS
##
## locale:
## [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
## [3] LC_TIME=pt_BR.UTF-8 LC_COLLATE=en_US.UTF-8
## [5] LC_MONETARY=pt_BR.UTF-8 LC_MESSAGES=en_US.UTF-8
## [7] LC_PAPER=pt_BR.UTF-8 LC_NAME=C
## [9] LC_ADDRESS=C LC_TELEPHONE=C
## [11] LC_MEASUREMENT=pt_BR.UTF-8 LC_IDENTIFICATION=C
##
## attached base packages:
## [1] parallel stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] klaR_0.6-12 Epi_2.0 MASS_7.3-45
## [4] glmnet_2.0-5 foreach_1.4.3 Matrix_1.2-6
## [7] mboost_2.6-0 stabs_0.5-1 knitr_1.12.3
## [10] latticeExtra_0.6-28 RColorBrewer_1.1-2 lattice_0.20-33
##
## loaded via a namespace (and not attached):
## [1] Rcpp_0.12.5 compiler_3.3.1 formatR_1.3
## [4] highr_0.5.1 plyr_1.8.3 iterators_1.0.8
## [7] tools_3.3.1 digest_0.6.9 evaluate_0.9
## [10] cmprsk_2.2-7 yaml_2.1.13 mvtnorm_1.0-5
## [13] coin_1.1-2 stringr_1.0.0 combinat_0.0-8
## [16] stats4_3.3.1 grid_3.3.1 survival_2.39-4
## [19] etm_0.6-2 rmarkdown_0.9.6 multcomp_1.4-5
## [22] TH.data_1.0-7 magrittr_1.5 codetools_0.2-14
## [25] htmltools_0.3 modeltools_0.2-21 nnls_1.4
## [28] splines_3.3.1 strucchange_1.5-1 quadprog_1.5-5
## [31] sandwich_2.3-4 stringi_1.0-1 party_1.0-25
## [34] zoo_1.7-13J. W. Smith, J. E. Everhart, W. C. Dickson, W. C. Knowler, and R. S. Johannes (1988). Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Symposium on Computer Applications in Medical Care , 261–265↩